
フェルミ推定の教科書【一歩差がつく回答編3】ディズニーランドの客数は?(1/3)
2019/05/28
会員登録すると
このコラムを保存して、いつでも見返せます

シリーズでお届けしている「フェルミ推定の教科書」。その中で、他の受験者と差をつけるためのコツをお伝えする【一歩差がつく回答編】ですが、【1】と【2】では、フェルミ推定に適切にアプローチするために、「商材理解」が重要であることを説明しました。
今回は、別の視点が重要となるフェルミ推定を取り上げます。
例題は、「ディズニーランドの来場客数」です。面接時間は、30分であると想定して、考えてください。
※この「ディズニーランドの客数は?」(計3記事)だけ読んでも役立つ内容となっています。
よくあるイマイチな回答例
最初に、「ディズニーランドの来場客数」のフェルミ推定にて、よくあるイマイチな回答例を一つ載せておきます。
Step1:来場者数を因数分解する
後ほど詳しく説明しますが、今回のフェルミ推定は、さまざまな因数分解のパターンが考えられます。
例えば、以下のような「アトラクション」を基準として因数分解するパターンが、よく見られる回答の一つです。
➢ (とある時間を切り取ったとき、)来場者数の過半数は、何かしらのアトラクションに、並ぶ・利用中であると推測されます。
➢ そのため、「アトラクションの数」と、「1アトラクションあたりの利用者・並んでいる人数」から、アトラクション関連の人数を割り出し、そこに「その他の客」を少し加えれば、(その時点の)来場者数が求められると思われます。
もう少し広い視点で考えられる人は、上記の因数分解に、以下のような層を追加できると思います。
➢ さらに、朝や夜しか利用しないお客さんもいると思われるので、その分を加えれば、1日の来場者数になると思われます。
以下、アトラクションを基準とした因数分解のイメージ図を載せておきます。
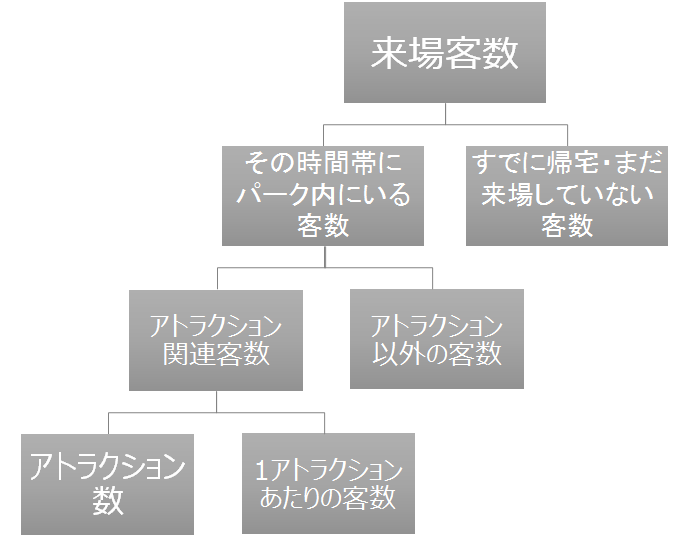
Step2:各値に数値を入れていく
その次は、上記のツリーの各項目に、数値を設定していくことになります。
例えば、アトラクション数だと、自分が利用した時の経験や知識を基に、「40施設」などと設定していくことになるでしょう。この数値は、パーク案内図のパンフレットを、なんとなく覚えていれば、大きく外れることはないと思います。
◆補足:必ずしも、数値を設定する必要はない。比率でもOK
少し話がそれますが、「アトラクション以外の客数」や「すでに帰宅・まだ来場していない客数」は、客数そのものの数値を設定するよりも、「比率」を設定したほうが良いでしょう。例えば、「アトラクション利用客数と、それ以外の客数は、1:1とします」といったイメージです。
絶対的な数値である客数を計算するよりも、相対的な数値である比率を計算するほうが、素早く設定できます。また、「1:1」「2:1」のように、比率のバランスに偏りがない場合、値を大きく外す可能性も低くなります。
このあたりは、原則編のコラムでも、「テイクアウト率」とイートイン率といった形で利用しました。無理に、絶対的な数値を計算するよりも、数値の大きなずれを防ぐことができ、また聞き手への納得度が高くなる場合も多いと思われます。
数値の設定方法も、「絶対的な値」「相対的な割合」のどちらが良いかなど、アプローチを工夫しましょう。
ありがちな回答例の問題は?
さて、上記のありがちな回答例は、どこに問題があるのでしょうか。以下、2つの問題点をあげておきます。
問題点1: そもそも、計算の量や精度が不十分
まず、計算の精度が低く、また計算量や分解された項目数も、面接時間に対して少なすぎるのが問題です。
◆30分の面接時間に対して、計算量・計算方法が大雑把すぎる
面接時間が、30分もあることを考えると、上記の分解では、大雑把すぎて、不十分な計算といえるでしょう。
5分で実施する概算であれば、上記のような大雑把な計算でも十分でしょう。
しかし、30分かけて計算を実施するのであれば、もっと細かく項目を分解し、さまざまな数値を設定することで、より精緻な計算を行うことが求められていると考えるのが自然です。
◆あいまいな数値が多く残っている
仮に、大雑把な計算方法でも、「十分に精緻な数値が計算できる」「これ以上細かい計算をしても、ほとんど予測精度が上がらない」のであれば、大雑把な計算方法でも問題ないといえます。
※ただし、そのような問題は、「20~30分の採用選考」として不適切なので、出題されないはずです。もし出題された場合、出題者の問題選定がイマイチという結論になってしまうのですが、そのような可能性は低いので、まずは自分の回答の質を疑ってみてください
しかし、上記の計算には、かなりあいまいな数値が残っています。
例えば、「1アトラクションあたりの客数」として、いきなり「1000人」と数値を置くのは、大雑把すぎるでしょう。もう少し細かい計算をして、精度を上げる努力をする必要があると思われます。単純に「1アトラクションあたりの客数」をもっと細かく分解した場合、例えば、「アトラクションのキャパシティ」「1回のアトラクション時間」「人気・列の長さ」といった分解が考えられます。
※ただし、後ほど説明しますが、これらの分解後の項目は、アトラクションの種類によって大きく異なるため、シンプルに数値を設定する(平均値を置く)のが難しそうです。
問題点2: 精緻な数値を設定することが難しい項目がある
問題点1を考慮すると、より精緻な計算になるよう、回答を修正する必要性が感じられます。例えば、因数分解や場合分けを、もう少し具体的・詳細にするなどの修正です。
しかし、結論を述べると、今回の場合、この「回答の修正・詳細化」が、なかなか難しいのが問題です。
以下、見ていきましょう。
◆因数分解式に、もう一軸入れて、マトリックス化するのが王道だが・・・
さて、より細かい数値を置いて、精緻に計算する場合、どのようにすればよいのでしょうか。
この場合の最も基本的な方法は、因数分解式に加えて、もう一つの軸を加えて、マトリックスとして、計算するという、原則編から、よく利用してきた対応策です。
回答編1の例題である、「缶ビールの市場規模」では、「アルコール利用頻度」や「居住エリア」が、場合分けの軸の候補となりました。このような、因数分解式の各項目の数値が、大きく変化するような軸を見つけて、場合分けするのが、基本的なアプローチといえるでしょう。
◆数値の予測精度を上げる、有意な2軸目が見つからない
しかし、「ディズニーランドの来場客数」の場合、予測精度を有意に上げそうな場合分けの軸が、なかなか見当たらないのが問題です。
そもそも、ディズニーランドのアトラクションは、個別にかなり特色があります。
そのため、すでに言及した通り、「1アトラクションの客数」は、アトラクションごとに、数値はもちろん、その背景となる要素も、かなり異なりそうです。仮に、因数分解の項目を細かくしても、一つの平均値に設定するのは、無理がありそうです。
そうなると、因数分解の項目を分解するだけでなく、2軸目で場合分けをして、「乗り物系」といった3~5個程度のグループに分けることになります。しかし、それでも、相当難しそうです。各アトラクションは、例えば乗り物系でも、一台のカートの定員も、アトラクション時間もバラバラです。面接官と、納得いく場合分けを議論するのは、かなりの高難易度になるでしょう。
グルーピングしないで解こうとすれば、個別・相当細かい分類で、数値を置いていくことになってしまいます。しかし、そうすると、逆に30分では終わらない推定になってしまい、非現実的です。
また、詳細は省きますが、「アトラクション以外の客数」を別途推定する必要がありますが、それらの各項目
➢ パレードを見ている・待っている
➢ 飲食店で食事・休憩中
➢ ショップで買い物中
➢ 施設内を歩行中(他の施設へ移動中or単純に散歩している)
といったあたりも、推定ロジックの作成が難しいです。

改善箇所: 因数分解式を見直す必要がある
上記の問題点を踏まえると、どのような対応・修正が必要になるのでしょうか。
まず、因数分解の方法に、見直す余地があると考えるのが自然です。
予測精度がイマイチな項目がある場合、因数分解式を見直す
原則編の「カフェの一店舗当たりの売上」にて、需要ベースでは計算が難しいという話をしたのを、覚えているでしょうか。その理由は、「商圏」という項目が、以下のような理由から、うまく数値を設定できないというものでした。
➢ 商圏を、半径500mとするか、2kmとするかで、16倍変わってしまう
➢ 一軒家か、マンションかによって、単位面積当たりの住民数が、大きく異なる
上記の、「1アトラクションあたりの客数」もまさしく、この商圏と同じような項目といえるでしょう。
このように、他の切り口を入れて、場合分けしても、精緻な数値にするのが難しい項目が存在する場合、因数分解の切り口が、あまりよくないと考えるのが自然です。
今回の場合、少なくとも、上記の「1アトラクションあたりの客数」は、精緻な計算が難しい項目であるように思えます。
5分で概算するなら、「とりあえず1000人」くらいの設定でもよいでしょうが、30分という面接時間に耐えうるような方法ではないと言えます。
そうなると、因数分解式を見直すことが必要と判断せざるを得ないでしょう。
ポイント: どのような因数分解でも、イマイチな場合はどうすべきか
さて、上記のような理由から、因数分解式を見直すことになります。その時、他にもっと良い因数分解式がないかという視点で、検討を進めることになるでしょう。
ここで、今回の「ディズニーランド入場者数」のフェルミ推定の特徴・結論を先に述べてしまいます。
実は、このケースの最大の難しい箇所は、「どの因数分解アプローチを選択しても、微妙な部分が残る」ということにあります。つまり、上記の「アトラクション」以外の因数分解の方法を探しても、おそらく「みんなが納得」するような、良い因数分解式は、存在しないということです。
なぜ、どの因数分解でもイマイチなのか、次回の「ほかの因数分解式」を示す箇所で詳細を説明しますが、このような場合、「どうやって因数分解式を決めるべきか」を判断するのは難しいといえるでしょう。
この、「ディズニーランドの入場者数」のフェルミ推定は「どの因数分解式もイマイチ」という前提をもとに、次の解説の「どのように因数分解式を決めるのか」を読んでください。
会員登録すると
このコラムを保存して
いつでも見返せます
マッキンゼー ゴールドマン 三菱商事
P&G アクセンチュア
内定攻略 会員限定公開
トップ企業内定者が利用する外資就活ドットコム
この記事を友達に教える


