フェルミ推定の教科書【原則編 2/7】Step2 振れ幅の大きい項目を細かく分解：ケース面接で他の学生と差がつくポイントとは？

本コラムでは、前回に引き続き、「とあるカフェ一店舗の売上金額は？」というフェルミ推定の回答例に沿って、ケース面接で「やりがちな間違い」や「差がつくポイント」を解説していきます。

ここまでのコラムを読んでいることが前提ですので、併せてご覧ください。

今回の記事の要点は下記5点です。

【Step2】 より振れ幅が大きそうな項目を、細かく分解していく

さて、「ポイント1」の考え方に従って、「Step1」で考えた売上金額を細かく因数分解していきましょう。例えば、以下のようになります。

・売上金額 = [客数] × [客単価]
・客数 = [席数] × [席の占有率] × [席の回転頻度] × [営業時間]

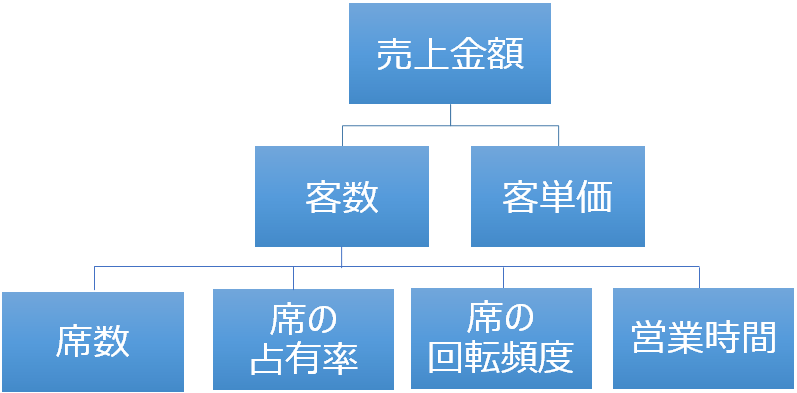
さて、イメージを持っていただくため、いきなり回答例を見せましたが、この部分については、以下のように、いくつか難しいポイントがあります。

これらを順次解説していきましょう。

【やりがちなミス】 知っているフレームワークを、当然のように当てはめて分解してしまう

例えば、あなたが「ラーメン屋の売上推定」というフェルミ推定の回答例を、何かで見たことがあるとしましょう。一見すると、今回の「カフェの売上推定」と非常に似ているように見えます。

「ラーメン屋の売上推定」の解説では、上記のような、「席数、占有率、回転頻度、営業時間」の切り口で解説されていたとします。さて、この切り口をそのままカフェの問題にも当てはめてよいのでしょうか？

【ポイント2】式の分解の切り口は、複数パターンを考え、比較検討する

さて、最初の「数」×「単価」レベルの分解は、「客数」×「客単価」、「ユーザー数」×「利用金額」など、多少の表現の差はありますが、選択肢も少なく、大きな違いは出ないと思います。

しかし、この「数」の分け方については、かなり差が出るので注意が必要です。

まず、今回の例題の分け方は、「席」に着眼しており、大きな括りで見れば、お店の持つ「供給」で見ていると言えます。しかし、「供給」視点で見る場合に限定しても、他にも「レジ」を着眼点に考えることができます。
※特に、今回のスターバックスの場合、後述する理由から、レジ起点で考えた方が、より切り口かもしれません。

また、詳細は省略しますが、企業側の「供給」ではなく、消費者の「需要」で見ることもできます。

MECEであることは当然。さらにその先が重要

計算式の分解と言われると、ついついMECEであればよいと考え、今回の例だと「席の回転頻度」などの「各項目に抜けがない」ことが満たされていることを確認して、検証が終わりがちです。

しかし、このMECEであること程度は、大抵の人はクリアできており、ここが問題になることは少ないです。

因数分解の切り口は、きわめて重要かつ大きな差がつくポイント

たとえ、MECEであったとしても、この因数分解の切り口がイマイチだと、今後の議論が難しくなり、面接の評価も悪くなります。ここは、かなり難易度が高く、様々なフェルミ推定を比較しながらでないと、解説が難しいです。

この部分をどのように考え・アプローチするべきか、問題の性質によって異なります。詳しくは、別途「テクニック編」で個別に解説していきます。

また、本解説では、いったんは、上記の数式の分け方が正しいものとして、解説を進めていきます。

 

【やりがちなミス】 すべて、ツリー構造で分解してようとする

さて、このコラムを読んでいる人は、「イシューツリー」「ロジックツリー」などと言われる、樹木構造による分解・論理思考の手法を知っている方も多いと思います。

さて、樹木構造に従って分解していくと、これ以上の分解が難しそうに見え、ここで数式の分解を終えてしまいそうになります。しかし、「ポイント1」に従ってみたとき、曖昧な・振れ幅が大きい箇所は、なくなったといえるのでしょうか。少し考えてみましょう。

【ポイント3】現実感のある議論をするため、知っている例を、具体的にイメージしてみる

さて、ここでは、数式の分解という「抽象的な思考」から離れて、スターバックスの実際の店舗の様子を「具体的にイメージ」してみましょう。

（スターバックスに行ったことがない人は、ドトールなどの、他のカフェ・チェーンで結構ですので、店舗の様子をイメージしてみてください）

「席の占有率」は、「時間帯」によって違いが大きい

さて、スターバックスを利用している時を、普段の利用店舗でイメージしてください。同じ店舗でも、「時間」や「店舗」によって、席の埋まり具合が大きく異なることがわかると思います。

もう少し、「時間」の側を具体的に考えると、「朝は比較的すいている」「お昼は混んでいる」「休日はすいている」などといった特徴が出てくるのではないでしょうか。つまり、「時間帯」や「曜日」の切り口が重要そうです。

そうなると、「席の占有率」は触れ幅が大きく、「50%」のような、一つの数値で設定することは難しそうであることがわかります。

やりがちなミス： 論理思考という名の抽象的な思考ばかりを実施してしまう

論理思考・ロジカルシンキングと言われると、「イシューツリー」「MECE」などといった単語が頭に浮かびます。これらは、いずれも「抽象的」な思考であるため、論理思考と言われると、ついつい抽象的な思考ばかりに目が行きがちです。

しかし、抽象的な思考を行うための基礎部分として、あくまで「具体的なイメージ」の実施が重要です。これは、ビジネスだと「現場感覚」などとも言われています。

ケース面接としていると、ついつい抽象的な「机上の空論」ばかりを実施してしまいがちです。適時、「目をつぶって具体的なイメージをしてみる」などの、抽象的な思考とは対極にある「具体的思考」によって、正しく状況や論点を把握してください。

テクニック： 具体的にイメージするときのポイント

いきなり、「具体的にイメージしましょう」と言われても、うまく実施することが難しいでしょう。コツは、「“プロセス”を“時系列”にて、順を追ってイメージする」ことです。

例えば、今回のスターバックスであれば、「1週間の利用タイミング」や「これまでの人生の利用経験」などの利用オケージョンを、順を追って整理してみるのです。

また、もっと細かいイメージとして、「スターバックスを利用するときの、1回の流れをイメージする」というものがあります。例えば、以下のような内容です。

※後ほど言及しますが、このようにイメージすることで、「席に座る（イートイン）だけではなく、テイクアウトがあるのでは？」「席の占有率や回転よりも、レジの回転をベースとする方が良いのでは？」などといった視点が出てきやすくなります。

具体的にイメージすることで、大きな見落としを防ぐことも可能になる

上記のように、具体的にイメージすると、根本的な見落としを防ぐことも可能になります。例えば、今回の回答例の数式の分解には、「テイクアウト」の視点がすっぽり抜け落ちていますが、この具体的イメージを経ることで、その視点に気が付きやすくなります。

※補足：この「テイクアウト視点」ような、大きな見落としは、「カフェの存在する数」といった「存在する数」を求めるフェルミ推定で、良く起こる傾向にあります。詳細は、例題編にて、適時解説します。

「具体的イメージ」は適時実施

また、この「具体的イメージ」によってわかったことは、ケース面接中の様々なStepで活きてきます。問題に対する理解が足りないと感じたタイミングで、適時「具体的イメージ」を膨らませて、理解を補強してください。

この後の解説でも、この「具体的イメージ」で分かったことについて、随時言及していきます。

※また、今後の解説は、いったん、まだこの時点ではテイクアウトの視点に気が付いていないものとして、進めていきます。

【ポイント4】ツリー構造だけでなく、2軸のマトリックスも活用しながら整理し、面接官と議論する

さて、話を戻しましょう。上記の「ポイント3」の議論から、「各項目の曖昧さ・振れ幅が大きくなる原因」である「時間帯」の切り口を反映したいところです。

しかし、この切り口を上記の「ツリー構造」の中に入れることは難しそうです。

（※補足：回転頻度や客単価も、時間帯によって異なる。ランチ時間であれば、回転は速く、単価も食事がある分だけ高い。時間帯によって、様々な項目の値が大きく変化するため、重要な切り口といえる）

1軸だけでは、複雑な事象の議論が難しい。2軸目を加えて、議論しやすくする

このような場合、ツリー構造にこだわるのではなく、「2軸のマトリックス」で考え、表現しながら議論することが有効です。

当然ですが、世の中の事象は複雑であり、様々な切り口によって変化します。このようなものを、1つの軸だけで、きれいに表現することは困難です。だからと言って、10個の軸で表現しようとしても、10次元の図を書かなければならず、現実的に表現不可能です。バランスをとって、2軸で考えるような癖をつけるのが現実的です。

2軸目は、1軸目の「差が大きくなる」軸を選ぶ

では2軸目は何を選ぶべきでしょうか。議論の流れで、大抵の場合1軸目は決まっています（今回の場合、売上金額を分解した式）。そのため、2軸目は、「1軸目の各項目の差が大きくなる」切り口を選ぶとよいでしょう。

今回の例の場合、「時間帯」が最もよさそうです。例えば、以下のように分けられるでしょう。

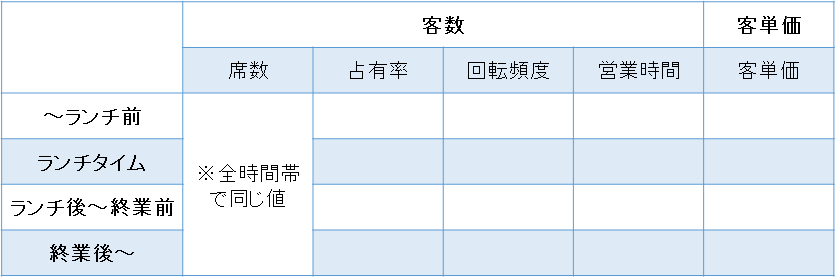
※テクニック： 「単位当たり回数」の部分を深く考え、差が出る2軸目を考える

さて、一般化して考えた場合、分解時の「数」を、より細かく分解すると、下のようになるでしょう。

※今回の例題との対応関係は、以下の通りです。

 

この時、基本的には「単位当たり回数」の部分が、別の軸によって大きな差が出ることが普通です。まずは、単位当たり回数をベースに、より良い2軸目がないか、検討しましょう。

さらに述べれば、2軸目の切り口も、以下の2種類のどちらかを利用することが多いです。

詳しくは、例題編で随時解説しますが、まずは上記の切り口を意識してみるとよいでしょう。

【やりがちなミス】 2軸目を、いきなり定量的な数値で設定してしまう

さて、2軸目として、「タイミング」や「ユーザーセグメント」を利用することが多いという話をしました。このとき、よくありがちな回答として、ここを、定量的な数値でいきなり設定するというものがあります。たとえば以下のような分け方です。

「数値設定のロジック」と「2軸目の分け方」に、不整合が発生していることが多い

さて、なぜこの方法がまずいのでしょうか。ここからは、年齢の分け方で考えてみましょう。

「年齢」の分類ごとに、カフェ利用率を左右する「特徴」を考えてみる。

まず、「0 - 19歳」のカフェの利用率をどう設定するでしょうか。簡単な例をあげると、「高校生までは、なかなかお金もないため、利用率は低い（大学生以降は、バイトなどでお金もあるため、利用率が上がる）」などです。

また、「60歳以降」のカフェ利用率であれば、「すでに定年退職後であり、平日は働いていない方々なので、利用できる時間帯が広いです。また時間的な余裕もあるため、・・・」、といった議論になるはずです。

「年齢」の分類と、各分類の「特徴」に不整合が発生している

しかし、考えてほしいのですが、この場合、年齢の分け方が、若干不自然です。

まず、「高校生までは・・・」といった議論をするのであれば、年齢の幅は「0-18歳」などとすべきでしょう。

また、「定年後は、平日働いていないため・・・」という議論であれば、「定年延長」を考慮して、「65歳以上」とするのが適切かもしれませんし、そもそも「定年後」よりも「平日働いていない」という特徴が重要なのであれば、「専業主婦の女性（60歳未満を含む）」などを、加えるべきともいえるでしょう。

つまり、最初に分けた、「年齢」の分類と、各分類の特徴の議論に、若干の矛盾が発生してしまっています。これでは、論理的な説明とは言えないでしょう。

なぜ、このような、おかしな分類になってしまうのでしょうか。それは、あるべきプロセスが1つ抜けているからです。

【ポイント5】「定性的な分類 ⇒ 定量的分類 ⇒ 数値に落とす」という順序を経ながら考える

そもそも、どういうプロセスで実施すべきだったのでしょうか。

まず、回答例を先に説明します。結局、「高校生までは、お金がない」「平日働いていない」などというのであれば、それに合わせた分類を実施すべきでしょう。たとえば、下記のようなセグメントに分けます。

そして、上記の各セグメントに対して、「年齢」や「性別」を利用した定義をすればよいでしょう。一例をあげると、大雑把ですが、以下のような定義です。

※セグメント分類だけでは、各セグメントにおける、定量的な人数を推定できません。そのため、「年齢」「性別」などの、定量的な数値に変換しやすい特徴を、各セグメントに定義しています。

重要なのは、年齢という定量数値ではなく、その定性的な特徴である

改めて確認すると、ケース面接として実施されるフェルミ推定において重要なことは、数値計算ではなく、数値を利用するときの「思考力」です。

その視点で見ると、重要なのは、あくまで「カフェの利用率」を左右する特徴であり、それは、例えば、ユーザーの特徴によって出てきます。このユーザーの特長が、年齢を切りよく区切った分類によって、うまく定義できるとは思えません。

あくまで、定性的に、「カフェ」というテーマの特長を考えた分類を、うまく考え出す必要があります。いきなり定量的な分類にするのではなく、まずは定性的な特徴から定性的な分類を考え、次に定性的な分類を定量に落とすための分類（年齢、性別、時間など）を付与し、最後に定量的な分類を基に数値にするという思考プロセスを忘れないでください。1番最初のプロセスが抜けがちなので、注意です。

上記のやりがちなミスは、1番最初のプロセスがないまま、年齢などの数値の区切りを設定したため、境目がおかしくなってしまったと判断できるでしょう。

特に、2軸目において、この問題が発生しやすいので注意する

フェルミ推定の全体において、この考え方を忘れずに実施してください。しかし、このミスがよく発生するのは、この「2軸目を設定するとき」であることを、特に意識しておいてもよいでしょう。「定量的な数値」で、軸が設定されている場合、それが本当に「重要な切り口」をベースとしたものになっているか、確認するようにしてください。

では最後に、今回の記事の要点を改めてまとめると下記5点です。

さて、次回のコラムでは、次のStep3の解説を行っていきます。併せてご覧ください。