フェルミ推定の教科書【テクニック編 4/6】例題5 都のカフェ市場の売上 ＆ 例題6 スタバ全店の売上 ＆ 例題7 デカフェコーヒーの売上：ケース面接における数式分解の適切なアプローチとは？

本コラムでは、前回に引き続き、「応用編パートB」の3つの例題を解説していきます。

ここまでのコラムを読んでいることが前提ですので、併せてご覧ください。

今回の記事の要点は下記3点です。

例題による解説：応用編パートB

さて、基礎編の内容を踏まえつつ、応用編のパートBのフェルミ推定を見ていきます。

このパートでは、「例題1」の市場規模の計算に関連する応用パターンを見ていきます。基本的には、基礎編を応用することで解けるものばかりです。

この応用編パートBでは、「問題文を分解し、より一般的な広い概念（身近でイメージしやすい概念）に変換した“シンプルな問題文”からの示唆を、数式に反映する」という視点を学習していきます。使用する例題は、以下の3つです。

【例題5】 東京都のカフェ市場の売上

さて、この計算は「市場規模」というマクロ数値なので、需要ベースで計算するのがよさそうです。このテーマは、そんなに難しくないので、直感的に以下のように数式を分解できる方も多いでしょう。

・市場規模 = 「東京都の人口」 × 「カフェを利用する人の割合」 × 「利用頻度」 × 「単価」
※東京都は、近隣の都道府県から出勤してくる人がいます。彼らもカフェを利用するので、厳密には「東京都の人口」ではなく、「東京で働く・住む人の数」でしょう。このあたりも注意したい所ですが、このコラムの趣旨からは外れるので、一旦無視します。

問題文を分解⇒シンプル化したものと比較してみる

さて、もう少し論理的に、プロセスを踏んで考えてみましょう。

まず、「東京都のカフェ市場の売上」という問題文を、分解すると、「東京都」「カフェ」「市場規模」となります。

次に、試しに問題文をシンプルに改変してみると、「東京都」という単語を抜く、もしくは「日本全体」と置き換えて、「日本全体のカフェ市場の売上」という、例題1と同じ問題文にすることができます。

シンプル化した問題文との差分に注目して、式を作成する

元の問題文と、このシンプル化した問題文の差分は、「日本人口⇒東京都人口」という部分だけです。ということは、日本の人口を、東京都の人口へと制限すればよいことになります。例えば、以下のように計算式を立てることができます。

・「東京都の人口」 = 「日本人口」 × 「東京都に住む割合」

つまり、以下のように表現できるでしょう。

・市場規模 = 「東京都の人口」 × 「カフェを利用する人の割合」 × 「利用頻度」 × 「単価」
（※東京都の人口 = 「日本人口」 × 「東京都に住む割合」を適用して）
・市場規模 = 「日本人口」 × 「東京都に住む割合」 × 「カフェを利用する人の割合」 × 「利用頻度」 × 「単価」

感覚的ではなく、論理的なプロセスを経ないと、式の分解が難しい場合も存在する

今回の例題である「東京都のカフェ市場の売上」は、別に「問題文を分解⇒シンプル化」というプロセスを経なくても、自然と
・市場規模 = 「東京都人口」 × 「カフェを利用する人の割合」 × 「利用頻度」 × 「単価」
というように式を分解できる方が多いと思われます。

しかし、この後は、「問題文を分解⇒シンプル化」という視点が重要になってくる例題を取り上げます。

【例題6】 スターバックス全店の売上

さて、この問題も、多くのスターバックスの店舗の合計ですので、マクロ的数値に見えます。そのため、需要・消費者ベースで数式を分解してみましょう。

例題1と同様、需要側から普通に式を分解してみる

例題1の「カフェ市場の売上」と同じように分解すると、「カフェを利用する人の割合」「一人あたり利用頻度」を、全て「カフェ」から「スターバックス」に置き換えればよいでしょう。

・市場規模 = 「日本人口」 × 「スターバックスを利用する人の割合」 ×「スターバックスの1人あたり利用頻度」 × 「単価」

しかし、このスターバックスの利用割合や利用頻度は計算が困難です。そもそも、「ほぼ毎日カフェに行く人から、たまにしか行かない人」まで、また「スターバックスのみ利用する人、たまにスターバックスを利用する人、ほぼ競合のカフェしか利用しない人」まで様々います。

このあたりを場合分けしていると、議論が複雑になるため、計算そのものも難しくなりますし、面接官との話もかみ合いにくくなります。

さて、同じ需要ベースの考え方でも、別のアプローチ・式の分解方法はないのでしょうか。

問題文を分解⇒シンプル化しながら、式を分解してみる

今回の問題文も、分解⇒シンプル化のプロセスを経てみましょう。

まず、問題文を分解すると、「スターバックス」「市場規模」となります。

次にシンプル化してみましょう。この時、「スターバックス」というのは、広義でみれば、「カフェ」の一つですので、「カフェ」に置き換えてみましょう。

そうすると、「カフェ市場の売上」という、例題1と同じ問題文になります。

シンプル化した問題文との差分に注目して、式を作成する

元の問題文と、このシンプル化した問題文の差分は、「カフェ業態 ⇒ スターバックス」という部分だけです。ということは、カフェ業態を、スターバックスへと制限すればよいことになります。

数式への反映方法は、いくつか考えられますが、例えば、以下のように計算式を立てることができます。

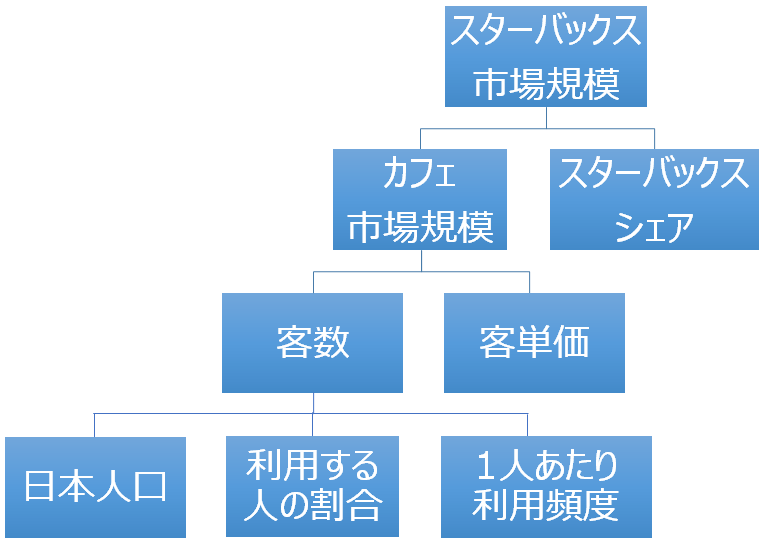
・スターバックス市場規模 = 「カフェ市場規模」 × 「スターバックスシェア」

その結果、以下のように表現できるでしょう。

・スターバックス市場規模 = [カフェ市場規模] × [スターバックス シェア]
・カフェ市場規模 = [客数] × [客単価]
・客数 = [日本人口] × [利用する人の割合] × [1人あたり利用頻度]

【例題7】 カフェ市場における、デカフェコーヒーの売上

さて、この問題も、デカフェコーヒーとありますが、あくまでカフェ市場における一部商品の売上に限定されているだけなので、マクロ的数値に見えます。そのため、需要・消費者ベースで数式を分解してみましょう。

例題1と同様、需要側から普通に式を分解してみる

例題1の「カフェ市場の売上」と同じように分解すると、「カフェを利用する人の割合」「一人あたり利用頻度」を、全て「デカフェコーヒー」に制限すればよいでしょう。

・市場規模 = 「日本人口」 × 「デカフェコーヒーをカフェで飲む人の割合」 ×「デカフェコーヒーの利用頻度」 × 「単価」

しかし、このデカフェコーヒーの利用割合や利用頻度は計算が困難です。そもそも、「デカフェコーヒーを飲む人から、飲まない人」まで、また「デカフェコーヒーを飲むが、インスタントを利用しており、カフェでは飲まない」など、様々なパターンがあります。

このあたりを場合分けしていると、議論が複雑になるため、計算そのものも難しくなりますし、面接官との話もかみ合いにくくなります。

さて、同じ需要ベースの考え方でも、別のアプローチ・式の分解方法はないのでしょうか。

問題文を分解⇒シンプル化しながら、式を分解してみる

今回の問題文も、分解⇒シンプル化のプロセスを経てみましょう。

まず、問題文を分解すると、「カフェ」「デカフェコーヒー」「市場規模」となります。

次にシンプル化してみましょう。この時、「デカフェコーヒー」というのは、「提供商品」の一つですので、「コーヒー・ドリンク」もしくは「全提供商品（食事やグッズを含む）」に置き換えられます。

いったん、「全提供商品」に置き換えると、「カフェ市場の売上」という、例題1と同じ問題文になります。

シンプル化した問題文との差分に注目して、式を作成する

元の問題文と、このシンプル化した問題文の差分は、「全提供商品 ⇒ デカフェコーヒー」という部分だけです。ということは、売上に入れる商品を、デカフェコーヒーのみへと制限すればよいことになります。

数式への反映方法は、いくつか考えられますが、例えば、以下のように計算式を立てることができます。

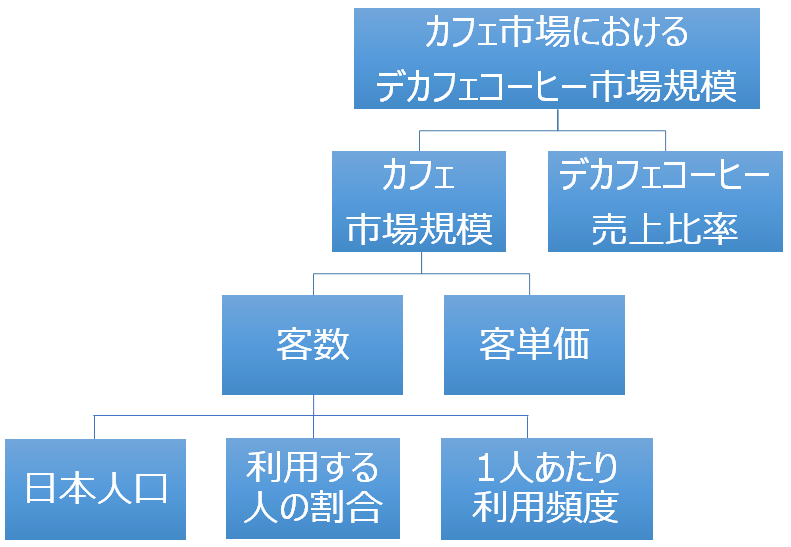
・カフェ市場におけるデカフェコーヒー市場規模 = 「カフェ市場規模」 × 「デカフェコーヒー 売上比率」

その結果、以下のように表現できるでしょう。

・カフェ市場におけるデカフェコーヒー市場規模 = [カフェ市場規模] × [デカフェコーヒー 売上比率]
・カフェ市場規模 = [客数] × [客単価]
・客数 = [日本人口] × [利用する人の割合] × [1人あたり利用頻度]

※補足： より議論しやすい式に、少し改変する

余談ですが、もう少し細かく書くと、カフェは、ドリンクだけでなく、食事も提供しているため、
・デカフェコーヒーの売上比率 = 「コーヒーの売上比率」 × 「デカフェコーヒーの選択比率」
という分解も考えられます。

また、そもそもデカフェコーヒーの取り扱いがないチェーン・店舗も存在するでしょう。

それらの概念を加味すると、
・カフェ市場におけるデカフェコーヒーの売上 = 「カフェ市場規模」 × 「デカフェコーヒー導入率」 × 「コーヒーの売上比率」 × 「デカフェコーヒーの選択比率」
としたほうが、イメージがしやすく、数字設定や面接官との議論がしやすくなるでしょう。

例題5、6、7のまとめ

さて、例題5、6、7、特に例題6、7を通してわかったことをまとめてみましょう。

そのまま式を分解すると、わかりにくくなる場合もある

スターバックスやデカフェコーヒーの事例で取り上げたように、「スターバックス」や「デカフェコーヒー」を前提とした、「利用する人の割合」や「利用頻度」を定義すると、議論が複雑になり、わかりにくくなります。

これは、序盤で解説した、「極端に小さい値を定義しなければならない項目を含む式の分解を避ける」という視点からも、同じことが言えます。「スターバックス」や「デカフェコーヒー」といった制限を付けると、「利用する人の割合」や「利用頻度」が小さい値になりやすいです。

また、「スターバックスを利用する人の割合」を、「カフェを利用する人の割合」「カフェ利用者の中でスターバックスを利用する人の割合」と2つに分解することも、もちろん理論上は可能です。しかし、利用頻度側も同じ分解が必要になるなど、パラーメータの数が多くなりすぎてしまい、また場合分けの議論（原則編の「ポイント4」 2軸のマトリックスで考える）も複雑になります。「不可能」とは言いませんが、あまり筋が良いとも言いにくいです。

問題文の制限事項を、できるだけ簡潔に式の分解へ反映する

そのため、もっとシンプルに、「スターバックス」や「デカフェコーヒー」などの制限事項を、計算式に反映したいところです。

例題6や7にある通り、直接テーマ（スターバックス、デカフェコーヒー）を計算しようとするのではなく、その一般概念である、「カフェ市場」を計算し、そこにテーマ特有の割合「スターバックスのシェア」や「デカフェコーヒーの比率」を適用した方が、分解式も、議論もスムーズになりやすいです。

補足ですが、この例題6と7は、「例題4：カフェの店舗数」と同様に、カフェの市場規模から「ツリーの1段上が増える」形式になっているため、普通に式を分解していくだけでは気が付きにくい計算式になっています。

その点から、応用編パターンAの例題3と4で解説した、「まず計算できそうな数値を洗い出し、それらを起点に考えていく」というアプローチに近いものがあります。

問題文を分解⇒シンプル化というプロセスを挟む

上記のような考え方を実施するためには、「問題文を分解し、より一般的・広い概念に変換したシンプルな問題文」をまず考え、「元の問題文との差分からの示唆を、数式に反映する」というプロセスを踏まえるとよいでしょう（例えば、例題6の場合、「スターバックス ⇒ カフェ」と変換しました）。

より一般的・広い概念は、身近でイメージしやすいものである必用があります。この身近でイメージしやすい問題文を起点に、そのシンプル化された問題文の目的数値に係数（例題6の場合、スターバックスのシェア）をかけるような、簡潔な形の式がないか、考えましょう。

最初に簡潔な分解方法を試したいが、あくまで面接官との議論で決定する

この「応用編パートB」では、制限事項（スターバックス、デカフェコーヒー）をよりシンプルに、数式へ反映する方法を示してきました。

しかし、「基礎編」でも言及した通り、つねにこの方法が正しいわけではありません。テーマ（カフェ）や制限事項（スターバックス、デカフェコーヒー）によって適切さが変わってくるのはもちろんですが、面接官がどう考えるかも重要です。

繰り返しますが、フェルミ推定は、あくまで「思考力を見るテスト」として実施されているにすぎません。面接官が、「スターバックスのシェアで、簡略的に計算するのではなく、もっと細かく・複雑な計算を実施してほしい。利用割合や利用頻度に絡めて、より細かく検討するときの思考プロセスが見たい」と考える可能性も十分にあります。

そのため、やはり両方の計算方法があることを提示し、それぞれのメリット・デメリットなどを議論できるようなプロセスを踏むのがベストでしょう。

【数式分解のアプローチ】 第3段階

さて、応用編パートBの3問からわかったことを加えたうえで、フェルミ推定における、数式分解時のアプローチをまとめておきましょう。

それでは最後に、今回の記事の要点を改めてまとめると下記3点です。

さて、次回のコラムでは、「発展編」として、2つの例題に対する、式の分解アプローチの解説を行っていきます。併せてご覧ください。