一歩差がつくフェルミ推定対策｜缶ビールの市場規模を推定してみよう！実践編①

実践を意識してフェルミ推定を解いてみる

「フェルミ推定の教科書」では、これまで以下の内容を扱ってきました。

上記では例題を基にフェルミ推定の解き方を解説してきましたが、本番のケース面接で応用できるようにするためには自分の頭で考えて、実践を積むことが大切です。

「ビジネス理解」がケース面接の鍵になる

実際のケース面接は、「採用選考」なので、受験者間で差をつけるため、少し「ひねり」や「ひっかけ」があることが少なくありません。これから説明していきますが、「ビジネス理解」、特に「商材の理解」がしっかりしていないと、「ひねり」「ひっかけ」をクリアすることができず、評価が低くなってしまいます。

上記のことを踏まえながら、例題を通じてより良い思考法を習得していきましょう。

今回の例題は「缶ビールの市場規模」です。面接時間は30分であると想定してまずは自分で考えてみてください。

ありがちな回答例を元に改善点を考えてみよう

よくある回答例

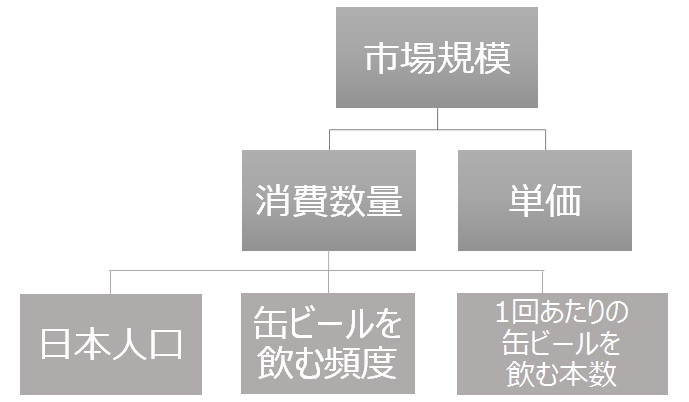
ざっくりと因数分解して数値を当てはめる

以下のような因数分解を行うのが、よくあるパターンです。

それぞれの要素に数値を入れていくのが次のステップだと思います。

日本人口は、一旦「1億2000万人」として、その次の「頻度」が問題です。仮にここを「1週間に2回」と置いた場合、どうなるでしょうか。
おそらく面接官から、「もう少し詳しく考えて」という質問を受けるはずです。

値の精緻化のために場合分けを行う

そうすると年齢を軸にして、下記のようなマトリックスを書き出す人が多いです。

そして、このマトリックスの各項目の数値を、順次埋めようとします。
※明らかそうな部分については、すでに上記のイメージ図に値を入れておきましたが、それ以外の部分については、面接官と細かい議論をしながら、数値を設定していくことになるでしょう。

さて、このよくある回答例の改善点を少し考えてみましょう。

改善ポイント①｜「缶ビール」という商材の特徴を踏まえた分解にする

上の因数分解では、缶ビールでなくても当てはまる一般化されたものなってしまっています。

例えば、「缶ビール」という部分を、「ガム」や「クリーニング屋」といった商材に置き換えても成り立ちそうです。

どの商材に変えても成り立つということは、「対象の商材の特徴を何も押さえていない」と言えます。

そのため「缶ビール」について何も考えていないことになり、他の受検生と差がつかない平凡な回答になってしまう可能性が高いです。「缶ビール」に特有の因数分解がないのかを考えてみて下さい。

改善ポイント②｜セグメンテーションが適切かを考える

そもそも因数分解した「頻度」「1回あたりの量」などに1つずつ数値を設定するのではなく、わざわざ（年齢などで）場合分けしたうえで数値設定するのはなぜでしょうか？

すでに、「フェルミ推定の教科書【原則編 2/7】」でも説明しましたが、その理由は、より正確・詳細に数値を設定して予測精度を上げるためです。

すぐに年齢や性別でセグメンテーションをしない

このような場合分けが必要なときに、すぐに「年齢」や「性別」でセグメンテーションをしてしまう人が多いですが、商材が缶ビールであることを考えると、このような分け方は正しいといえるでしょうか。

「20-39歳」と「40-59歳」とで何が違うのでしょうか？「60歳以降」も多少変わるでしょうが、大きな違いになるとは思えません。

後ほど説明する通り、缶ビールという商材を踏まえた、より適切な切り口があるはずです。

商材を意識してもう一度考えてみよう

ありがちな回答例は無難でひねりがないため、他の就活生と差をつけることができません。
すでに改善ポイント①②でも述べた通り「商材の特徴を理解すること」が一歩差がつく回答を出せるようになるための土台です。

「原則編2」にて、「【ポイント3】現実感のある議論をするため、知っている例を、具体的にイメージしてみる」という話をしましたが、「商材の特徴」を把握するためには、このような思考を、しっかり持つよう意識することが重要です。

では、今回のお題「缶ビールの市場規模推定」の場合はどうすれば良いでしょうか？

プロセス①｜「需要」と「供給」どちらからアプローチするのかを決める

商材が消費財の場合、需要ベースで考えていくのが基本

今回は商材が缶ビールのため、「需要ベース」か「供給ベース」かで考えたとき、圧倒的に「需要ベース」の方が考えやすいです。

供給ベースだと数の検討がつきにくい要素が多く、数値の振れ幅が大きくなってしまうのに対し、需要ベースであれば、消費財の場合は数値設定のイメージがしやすくなります。

ここは少し型にはまった考え方になってしまいますが、基本的に【消費財の場合は需要ベースで考える】といいでしょう。もちろん、供給ベースからでも良い回答が出せる場合もあるのですが、思考時間が限られているため、一旦は需要ベースでアプローチしてみましょう。

プロセス②｜「缶ビールの特徴」を理解する

需要ベースで考えるという方向性は決まったものの、ここから細かく因数分解をしていくためには商材である缶ビールの特徴を考えることが大切です。
しかし、いきなり特徴を考えてと言われても難しいので、ここではコツを紹介していきます。

缶ビールの位置付けを抽象化して考える

出題文には「缶」という制限がかかっています。こういった細かいこともしっかり考えていくのが良い回答を出すためのポイントです。
缶ビールの位置付けを明確化するために、抽象化していきましょう。

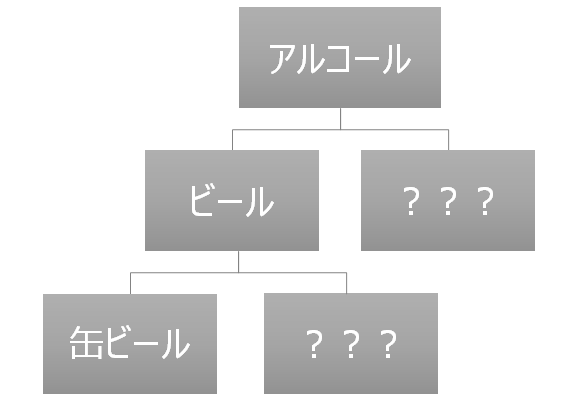
抽象化をもとに具体的な位置付けを考える

上の図のような分類をしたとき、「？？？」の部分を考えることで缶ビールの具体的なポジションが見えてきます。
ビール以外のアルコールに何があるのかを考えるために、普段よく行く居酒屋のメニューなどを想像してみて下さい。「ハイボール」や「日本酒」など様々でてくると思います。

さらに一段、ビールを具体化して「缶ビール」以外のビールがあるのかを考えてみましょう。「缶」は容器なため、容器の軸で整理してみると「瓶ビール」や「生ビール」が浮かぶと思います。

プロセス③｜他の商材と比較して、より深く特徴を考える

缶ビールの位置付けを整理しましたが、これをもとに他の商材と比較することで「缶ビール」の特徴を考えていくと、深掘りしやすくなります。

缶ビールはアルコールである

当たり前のことですが、これをしっかり頭の片隅に置いていることが大切です。アルコールであるという性質上、「飲める人」と「飲めない人」が存在し、このあたりの軸は缶ビールの市場規模の数値に大きく影響を与えます。

缶ビールと他のアルコールとの違いを考える

缶ビールの特徴は、結局何なのでしょうか。これは、ビール内の他の商材である「瓶ビール」「生ビール」と比較すると分かりやすいです。

これらの瓶や生の商品は基本的に「お店で飲む」ものですが、缶ビールは「家で飲む」場合がほとんどでしょう。

このように、ビールは、容器によって、飲む場所・オケージョンが異なるのです。

もちろん、上記には例外があり、缶ビールを出すお店もあります。家に瓶ビールやサーバーを置く人もいるでしょう。そのため、「基本的にはこうなる」という表現で伝えることになるはずです。

しかし、このような例外は「数値の推定」にほとんど影響がないため、あまり細かいことは気にせず、シンプルに考えましょう。
「サーバービール」「瓶ビール」などの「缶ビール」の競合を“明確”に意識できていることが、より重要です。

商材理解をもとに因数分解の修正を行う

「缶ビール」の特徴を押さえた切り口の設定

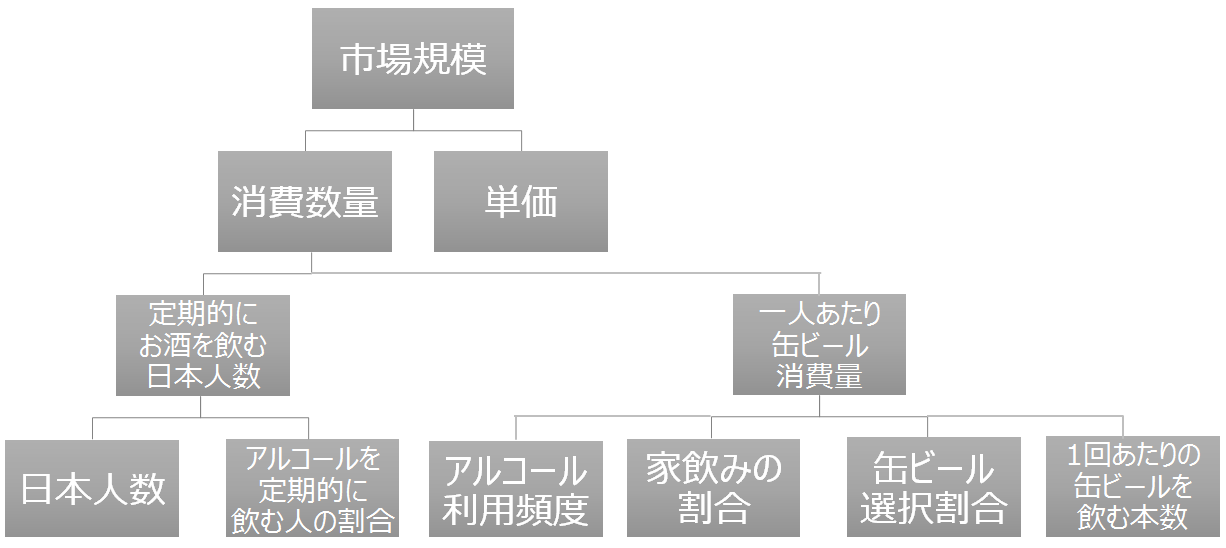
これまでの商材理解を踏まえると、例えば以下のように、より細かく缶ビール専用といえるような因数分解式を作ることができるでしょう。

さらに深掘りできそうな要素を詰めていく

上記の因数分解式の中で「アルコール利用頻度」や「家飲みの割合」はもう少し分解して考えることができます。「アルコール利用頻度」については以下のような切り口が考えられるでしょう。

ポイント①｜飲む場所の違いは、どの様な条件に左右されるのか

「家飲みの割合」については、家で場合とお店で飲む場合にどのような違いがあるのかを考えてみましょう。
ここで思考のジャンプが必要になりますが、「お店で飲むことができない人」について考えてみるのも一つです。

例えば通勤・通学方法に着目してみると、車で移動する人はお店でお酒を飲んでしまうと、運転できなくなってしまいます。
電車やバスで帰れない人は、他の人に運転してもらわなければなりませんが、これもかなり難しいです。つまり、車で移動する人の場合、上記のような制限から、「家飲み」という選択肢が必然的に増えるのです。

ポイント②｜車で通勤・通学する人は、どの様な条件・特徴の人か

車の代替手段は、自転車・徒歩などのスピードに限りがある手段を除くと、電車やバスになるでしょう。
しかし、「自宅」「職場・大学」の間を都合よく電車とバスで行き来できるのは、公共交通機関が発達している地域に住んでいる人だと考えられます。そのため、田舎の人ほど、夜にお店でお酒を飲むのは厳しそうです。

つまり、住んでいる・働いているエリアが、公共交通機関が発展している都会か、田舎かによって、家でお酒を飲む頻度は大きく変化しそうです。
このくらい深く考えれば、都道府県などに紐づけて、因数分解式に落としやすくなるでしょう。
ちなみに、それまでに出た切り口自体は、意味がないわけではありません。いきなり「都市部」「田舎」という切り口を示されても、聞き手からすると唐突に感じるでしょう。
このような、「家で飲む」「お店で飲む」や、「車で移動」「電車・バスで移動」といった切り口を経ていることを、しっかりと説明する必要があります。

商材理解ができていれば、その後の数値設定がスムーズに

因数分解したら、あとは数値を当てはめていくだけです。商材理解を因数分解の段階でしておくことで、面接官から「なぜそのような数値設定にしたのか？」と聞かれても、納得感のある答えが返しやすくなります。

今回の解説は以上です。くれぐれも、「因数分解」や「場合分け」をパターン的に行うのではなく、しっかりと自分の頭で考えましょう。そのときには、「商材理解」を深めることを心に留めておいてください。