フェルミ推定の教科書【テクニック編 6/6】例題9 ニューヨーク州におけるカフェ市場の売上：ケース面接における数式分解の適切なアプローチとは？

本コラムでは、前回に引き続き、発展編の2つ目の例題と、この「テクニック編」全体の総まとめを解説していきます。

ここまでのコラムを読んでいることが前提ですので、併せてご覧ください。

今回の記事の要点は下記3点です。

【例題9】 ニューヨーク州のカフェ市場の売上は

最後に若干「変則的」な問題を取り上げます。

まず前提として、あなたは、特にニューヨークに縁もゆかりもない（住んでいたこともなければ、旅行で行ったこともない）という前提で、この問題が出題されたと考えてください。
※ニューヨークに行ったことがある方は、ロンドン・ベルリンなど、よく知らない別の海外の都市をイメージしてください。

さて、あなたはニューヨークについて詳しくなく、細かいイメージができません。このような状況で、どのようにアプローチすべきでしょうか。今回は「知っている例から類推する」という視点を学習します。

需要サイドから、目的数値の式を分解してみる

まず、今回も、市場規模というマクロ数値なので、需要・消費者の視点から分解していきましょう。たとえば、以下のようになるでしょう。

・市場規模 = 「ニューヨーク人口」 × 「カフェを利用する人の割合」 ×「カフェの利用頻度」 × 「単価」

さて、ここからが問題になります。受験者は、ニューヨークについて、全然イメージがわきません。例えば、「ニューヨークの人が、どれくらい頻度でカフェを利用するのか」といった数値を、設定することができないのです。つまり、上記の分解された4項目は、設定が難しい数値となってしまいます。

このような場合、どうアプローチすればよいでしょうか。

とりあえず、問題文を分解⇒シンプル化してみる

さて、今回の問題分を分解すると、「ニューヨーク」「カフェ」「市場規模」といったあたりになります。

次に、この問題文をシンプル化した場合、読者が日本に住む日本人であれば、「日本」「カフェ」「市場規模」といった形になるでしょう。また、ニューヨークは都市なので、同じく都市である「東京」「カフェ」「市場規模」としてもよいかもしれません。

知っている例に対して、係数をかけて計算するのが現実的

さて、シンプル化した問題文に、「東京都のカフェ市場の売上」がありました。これは、例題5でも実施した通り、解くことができます。

この「東京都」と「ニューヨーク」の問題は、問題の構造が極めて似ています。

・市場規模 = 「東京都人口」 × 「カフェを利用する人の割合」 ×「カフェの利用頻度」 × 「単価」
・市場規模 = 「ニューヨーク人口」 × 「カフェを利用する人の割合」 ×「カフェの利用頻度」 × 「単価」

※さらに、両方とも、都市部であるため、少なくともカフェの店舗の形態（イートイン、テイクアウト、ドライブスルーの有無など）が似ていると想像できるでしょう。

東京都（日本一般）の計算式・数値設定を基準に計算する

改めて確認すると、フェルミ推定は、知っている情報な知識の範囲内で、目標としている数値を概算する計算です。このように、よくわかる例（東京都、もしくは日本一般）があるのであれば、それを基に類推していくのが良いでしょう。類推の背景のロジックを、係数として適用するのです。

例えば、以下の図のように、「論理的に設定する数値」に、「係数」の項目が加わるイメージです。

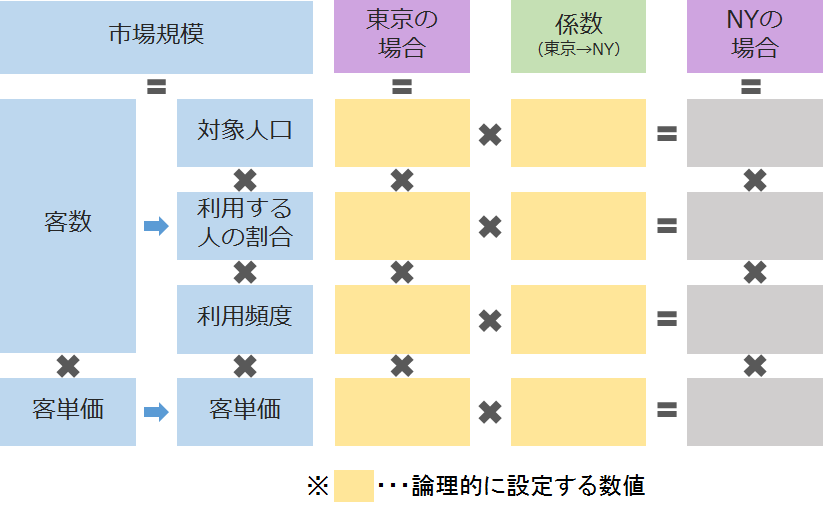
※「日本全体」でも、もちろん大丈夫ですが、同じ都市である東京都などに限定したほうが、よりニューヨークの状況に近づくでしょう。そのため、東京都の事例を基にした方が、より論理的かと思います。東京都や大阪府など、都市部のイメージがわく方は、いずれかの都市をイメージしましょう。

知っている例に対して、係数をかけて計算する場合の考え方の例

参考までに、今回の例題9に対する、知っている例に対して係数をかける場合のイメージを記載します。一部の項目だけでなく、ほぼすべての項目に、類推⇒係数をかけるというのが、ここまでの例題との違いです（例題6では、スターバックスのシェアという、1つの係数のみを利用しました）。

類推イメージ1：人口の場合

日本の人口は1億2000万人であり、東京都の人口は1200万人であるため、約10分の1を占めます。また東京都は47個の都道府県の1つです。

アメリカの人口は、明確に記憶していないかもしれませんが、約3億人という感覚はあるのではないでしょうか。ニューヨークの人口はわかりませんが、アメリカは約50個の州からできていること程度も知っている人は多いでしょう。

このため、日本と類推して、アメリカ人口の約10分の1の3000万人としておいても、大きなずれは発生しないでしょう。（日本は、東京の一極集中が進んでいますが、アメリカは他にも大きな都市がたくさん存在します。そのため、ニューヨークは10分の1よりも小さいとも考えられます。その程度のロジックを、さらに追加で入れてもよいかもしれません。）

類推イメージ2：カフェを利用する人の割合とカフェの利用頻度の場合

まず、東京都でカフェを利用する割合は、例題5を解くように、イメージから計算していきます。

一方、ニューヨークのカフェを利用する割合を直接イメージできなくても、東京とニューヨークの比較であれば、どうでしょうか。

まず、おそらく、アメリカのほうがコーヒーやカフェの本場なので、東京より、カフェを利用する人の割合は高くなるでしょう。また、カフェの利用頻度も、同じ理由で、アメリカのほうが高そうです。

この、数値が「高そう」「低そう」という感覚を、係数として設定していき、最後に、東京都のカフェ利用の数値にかけていくことになるでしょう。

類推イメージ3：単価の場合

ここは難しいのですが、いくつか視点があるでしょう。たとえば以下のような視点です。

両者の視点は、単価に対して、逆の示唆を示しているので、結論として、ニューヨークと日本のどちらが高くなるか微妙です。しかし、ケース面接において重要なのは、結果ではなくプロセス・考え方ですので、上記のような視点や論点と、それらが与える影響をしっかりと面接官に伝えて、議論しましょう。

3種類の類推イメージにて、視点の例をあげましたが、上記以外にも様々な視点が存在します。一度整理してみてください。

よくわからない数値は、類推⇒係数を活用する

改めて、今回の示唆をまとめておきます。

今回の場合、ニューヨークという極端な例を出しましたが、このようにイメージしにくいものがテーマとなることはよくあります。このような場合、まず知っている・イメージできるものを類推し、その類推との違いを「定性的」に考えた上で、係数を作成・適用することで、数値を計算することが有効です。

類推のその他の例： マッサージチェアの価格は

上記の例だけだと、類推に対する理解が難しいと思われますので、それ以外に、よくある類推の例を出しておきます。

例えば、「マッサージチェアの市場規模は」というフェルミ推定の場合、「数量・台数」もさることながら、「価格」の予測も困難そうです。さて、価格の予測をどう実施しましょうか。

例えば、コストベースなどは不可能と言って差し支えないでしょう。「部品の価格」や「組み立て費」を積み上げていくことが、短い面接時間内に可能だとは思えません。

それでは、類推によるアプローチはどうでしょうか。以下、他の商品と類推してみましょう。

類推1： オフィスチェアと類推する（価格の下限値）

まず、オフィスチェアの価格を考えてみます。オフィスチェアも、安物でなければ、「5万円10万円単位」の価格がすることは、知っている方も多いでしょう。

さて、オフィスチェアとマッサージチェアを比較した場合、さすがに、マッサージチェアの方が高いように思えます。つまり、マッサージチェアは、少なくとも、「5万円10万円単位」よりは高いと推測されます。

類推2： 軽自動車と類推する（価格の上限値）

次に、自動車と類推しましょう。自動車でも、軽自動車などで安いものを探せば、新車でも100万円くらいで買えるでしょう。さて、この「安い軽自動車」と「マッサージチェア」を考えた場合、さすがに、「マッサージチェア」の方が、“かなり”安いと思われます。つまり、マッサージチェアは、100万円よりも、“かなり”安いでしょう。

類推結果をまとめる

以上の結果から、10万円よりは高く、100万円よりは安いと推測されます。ここで、「ざっくり25万円」としても、おおきなズレはないでしょう。

類推の考え方は、高い思考力が問われる、有用な「思考力のテスト」である

このように、類推から、上限や下限を推定することは、数値の予測において重要です。

ちなみに、この「マッサージチェア」の問題は、上限と下限の両方を設定しました。しかし、例題9のニューヨークのカフェ市場規模の問題、特に「利用割合」「利用頻度」は、東京都の事例という「下限」のみを計算し、そこから類推しています。

このような「類推による考え方」は、「何と類推するか」「類推結果をどう解釈し、本題に適用するか」といった面で、思考力が問われます。「ニューヨーク⇒東京」の類推は、比較的簡単なレベルと思われますが、この「マッサージチェア」の類推は、「何と類推するか」を選択するのが難しく、難易度は高めです。

難易度が高いアプローチですが、困ったときは「類推で解決できないか」と考えてみてください。

【数式分解のアプローチ】 最終版

さて、全ての例題が終わりましたので、フェルミ推定における、数式分解時のアプローチをまとめます。

それでは、今回の記事の要点を改めてまとめると下記3点です。

まとめ： 因数分解のアプローチが、フェルミ推定の議論を大きく左右する

さて、ここまで見てきた通り、フェルミ推定の式の分解に対するアプローチは様々です。また、どのアプローチを採用するかに応じて、その後の議論の良し悪しが大きく変化します。

「需要と供給の両面から考える」「シンプル化した問題文と比較する」ことがベース

ここまで解説してきた通り、基本的には多くの分解アプローチを考える事、特に需要と供給の両方から考える事が重要です（例題1、2）。

それに加えて、問題文を直接解くのではなく、解けそうな問題を考える事も、アプローチ方法を広げるうえで有効です（例題3、4）。

特に、まずは「問題文を分解し、より一般的かつイメージしやすいシンプルな問題文」を考え、次に「シンプルな解きやすい問題文を解きながら、元の問題文と比較⇒差分を係数として計算式に反映させる」といった簡略化をすることで、解きやすくなることも多いです（例題5以降）。

また、このようなプロセスを経る中で、時には、事実上フェルミ推定を2つ解かなければならない場合（例題8）や、差分を係数とする部分が、1部の項目ではなく、ほぼすべての項目にわたる場合（例題9）もあります。

重要なのは、結論ではなく、アプローチや考え方。面接官との議論に重きを置く

ここまで、妥当な式の分解方法について解説してきました。しかし、式の分解方法は、「正しい解法」が1つに定まるようなものではありません。

本解説で出てきた妥当性は、あくまで私が考えるものであり、面接官によって考えた結果が異なってきます。

そのため、このシリーズの解説内容からは、結論ではなく、「どのようなアプローチのパターンがあるか」「どのように考えながら、妥当性を検討するか」といった「思考方法」を学習していただければと思います。

そして、実際のケース面接中は、「様々なアプローチを検討する」ことや、「それらのアプローチの妥当性を面接官と議論する」といった、柔軟な姿勢で臨むことを忘れないでください。

今後の進め方： 練習問題編（仮）による訓練

まず、この「テクニック編」を読んだうえで、再度「原則編」をご覧いただくと、より内容が理解できると思いますので、復習としてご確認ください。

この「テクニック編」で解説した、式の分解が無茶苦茶だと、この後の議論がきびしくなります。しかし、ここができていたとしても、その後に待ち受ける「数値設定」と「その設定理由」などの細かい議論でも、思考力の差が如実に出ます。詳細は、原則編にある、
・【ポイント4】ツリー構造だけでなく、2軸のマトリックスも活用しながら整理し、面接官と議論する
・【Step5】 なぜその数値を設定したのか、理由を説明する
をご覧ください。

まずは、因数分解を「思考力が低い」とは判断されないレベルを確実に抑えることで、その後のステップへつないでいただければと思います。

それ以降の細かい話は、ルール・一般化が難しいため、様々な問題を解きながら、帰納的に勉強するのが適切であると考えています。

「フェルミ推定の教科書」の【一歩差がつく回答編】で様々なフェルミ推定を解説していきますので、適時ご覧ください。