フェルミ推定の教科書【テクニック編 1/6】例題1 カフェ市場の売上：ケース面接における数式分解の適切なアプローチとは？

コンサルティングファームをはじめとした、様々な企業の採用選考で出題されるケース面接。多くの方が、以下のような課題をもっているのではないでしょうか。

以前のコラムでも解説しましたが、ケース面接、特にフェルミ推定では、「根本的なアプローチ」がイマイチであり、面接の序盤で、すでに厳しい状況に陥っている方が多いのが実情です。
※このような場合、面接官もどこからコメントしてよいか、判断が難しいため、「面接官の反応は悪くないのに、選考が通過できない」となります。

本シリーズでは、筆者が経営コンサルタントとして働く一方で、多くの学生・若手社会人の方と、1対1で、ケース面接練習を手伝いながら見出してきた、「よく“つまずく”ポイント」と「それを回避する」方法をカウンセリングしていきます。

導入： ここまでの解説と本コラムの位置づけ

「フェルミ推定の教科書【原則編】」（※【原則編 1/7】に遷移します）では、1つのフェルミ推定（カフェ一店舗の売上）を、ストーリーに沿って解説することで、どのような場所でつまずくのかと、解き方のポイントを、一通り解説しました。

その中でも、特に、「目標数値の分解に対する、適切なアプローチ」に関する「ポイント2」は、その後の議論に対する影響が大きい重要箇所であり、なおかつ受験者の間で、大きく差が付くポイントであることも、併せて言及しました。

そのため、フェルミ推定解説のテクニック編では、この「ポイント2」の詳細解説を行います。

前回までのコラムである、「フェルミ推定の教科書【原則編】」をご覧いただいた後のほうが、理解しやすいと思われますので、まだご覧になっていない方は、ぜひ原則編も併せてご覧ください。

今回の記事の要点は下記3点です。

本解説の進め方

この解説では、「カフェ」に関する様々な種類のフェルミ推定を、基本的なものから順番に利用しながら、「ポイント2」の式の分解に対する適切なアプローチを、学習していきます。使用するフェルミ推定の問題は、以下の通りです。

※特に指定がない場合は、「カフェの中に、“喫茶店”を含まない」「1年間の売上を求める」「日本に存在するカフェ」と考えてください。

2つの大原則： 複数パターンを考え、ボトルネックを意識して決定する

さて、例題を解説していく前に、まず、「大原則」を2つ示しておきます。例題の中で、まずは大原則を解説しながら、その他の原則を補足・追加していきます。
※この大原則は、抽象的な表現が多いため、理解しにくいです。詳細は、例題の中で説明していきますので、何となく意味をつかんでいただければ充分です。

大原則1： 必ず“両側”から考える（需要と供給より）

まず、1つではなく、“複数”パターンの分解式を考案できていないと、より良い式の分解方法を選択することは、現実的に困難です。この時、“両側”という全く異なった視点から考えることで、性質の大きく異なった複数の分解式が導出しやすくなります。

なかなか、抽象的な表現が難しいのですが、以下のようなイメージを持っていただけるとよいかと思います。

今回は、特に「消費者（需要）」 or 「企業（供給）」という視点をベースに解説していきます。

大原則2： 各項目の数値における、曖昧さや制限を考える

さて、「大原則1」で様々な目標数値の分解式を洗い出した後に、どれがより良い式かを選択する必要があります。この時の原則は、「曖昧さが大きすぎる（⇒計算が難しい）項目を含まない」というのが重要な判断基準です。

また、曖昧さを含まず、計算しやすい数値であるためには、「イメージしやすい、なじみのある項目である」ことや、「極端に小さい値でない」ことも必要です。以下、見ていきましょう。

需要（消費者目線）の場合

詳しくは、このあと「例題1」で解説しますが、特に「母数」にあたる項目の曖昧さが大きく、範囲を明確に定義できない時、この「需要」によるアプローチが難しくなります。

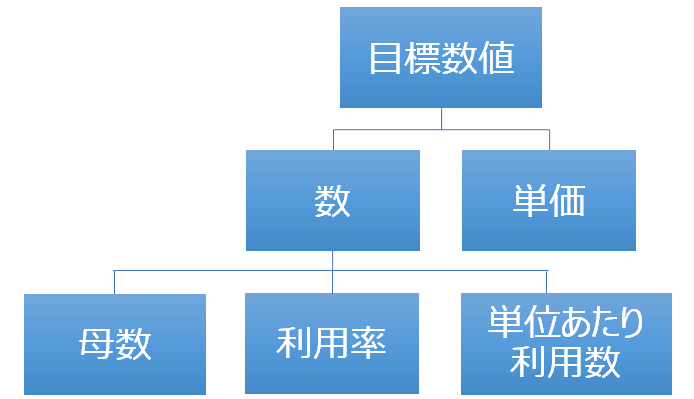
典型的な例は、「商圏人口」です。商圏は、範囲が明確でなく、難しいアプローチといえるでしょう。逆に、母数が、「日本人口」などのように、明確に定義できるものであれば、この「需要」による計算がしやすくなります。

また、「母数」以外の項目（利用率や単位あたり利用数など）については、「極端に小さい値になる」場合、イメージが難しくなるため、数値の曖昧さが大きくなります。「50%か10%か」をイメージして間違える可能性は低いですが、「0.5%か0.1%か」などの小さい値になるほど、イメージを的確に実施し、数値を予測することが難しくなります（どちらの例も、5倍の違いがあるため、最終結果に与える影響が同じです）。

以上のように、「母数が曖昧」な場合や、「極端に小さい値を定義しなければならない」場合は、別の切り口を考えた方が良いでしょう。

供給（企業目線）の場合

くわしくは、「例題2」で解説しますが、まず、供給視点が適している場合も、やはり曖昧さが大きな項目が存在しない事が重要なのは変わりありません。

また、供給サイドが適しているか否かは、「供給量のMAX値を明確に制限」できる部分を起点として、計算式が作成可能か否かにかかっている傾向があります。

例えば、一店舗のカフェであれば、「席数」や「レジ数」を超える商品・サービスの提供は難しいでしょう。

他には、「映画館」のフェルミ推定の場合であれば、同じく「席数」が供給制限になります。海外旅行・航空機なども、「空港数」「滑走路数」などの、明確な供給制限があります。

これらの供給の上限をベースに、供給側の稼働率を計算していくことで、計算の議論がしやすくなります。

大原則の解説は以上です。このような原則を読んでも、なかなかイメージがわきにくいと思いますので、早速例題をベースに確認していきましょう。

例題による解説：基礎編

では、早速、例題による解説に入っていきます。基礎編で使用するのは、以下の2問です。