フェルミ推定の教科書【原則編 6/7】Step6 数値の計算を実施：ケース面接で他の学生と差がつくポイントとは？

本コラムでは、前回に引き続き、「とあるカフェ一店舗の売上金額は？」というフェルミ推定の回答例に沿って、ケース面接で「やりがちな間違い」や「差がつくポイント」を解説していきます。

ここまでのコラムを読んでいることが前提ですので、併せてご覧ください。

今回の記事の要点は下記3点です。

 

 

【Step6】 数値の計算を実施する

さて、分解した数式の各項目に数値を設定し、面接官にその理由を説明し終わりました。

そのため、とうとう数値を計算していくことになります。

もちろん、計算ミスしないように気を付ける必要がありますが、それよりも重要なことは、「計算方法を工夫する」ことです。「計算方法の工夫」であれば、「論理的思考」の要素が絡みます。

【ポイント12】正確に計算するのではなく、だいたい正しい値になるよう計算すればよい

この部分は、ほかのケース面接対策のコンテンツでもよく言及されるためか、しっかりと実施できている方が多いです。しかし、念のため補足・言及しておきます。

数値を大雑把に丸めて計算する

フェルミ推定の目標を再確認すると、あくまで目標とする数値を「概算」することです。そのため、ここまでの議論において、設定してきた数値は、ある程度大雑把なものでした。

そもそも、設定した数値が大雑把である以上、その大雑把な数値を基にした計算を厳密に行っても、あまり意味がありません。

例えば「19×32」といった計算をそのまま実施すると面倒ですが、「19⇒20」「32⇒30」と数値を丸めてしまえば、「20×30」となり、計算が簡単になります。

別の例だと、「（20 + 30 + 1）×（3 + 5 + 0.1）」などといった計算は、[1][0.1]あたりの数値を無視しても、たいして結果は変わらないため、「（20 + 30）×（3 + 5）」と簡略化しても問題ないでしょう。

このあたりは、効率的な計算方法の話なので、フェルミ推定の練習をしなくても簡単に実施できるはずです。苦手な方は、おそらく、ケース面接前の筆記試験を突破することが、そもそも困難になると思われますので、計算ドリルのようなもので、早めに基本的な四則演算を訓練してください。

練習時は、数値を厳密に計算するのではなく、概算した結果が解答とだいたいあっているか否かを、正解の基準とするとよいでしょう。

あくまで数値の計算ではなく、その段取りというアプローチを見ている

再度確認しますが、計算の正しさよりも、計算の段取りの良さなど、アプローチを見られていると心得ましょう。段取りの良さも、論理思考の一つです。

 

【やりがちなミス】 全てのパターンをフェルミ推定しようとする

さて、テーマは「カフェ1店舗の売上金額」ですが、計算が1種類で済むとは限りません。

例えば、ここまでの計算は、「イートイン」のみを対象としてきましたが、「ポイント3」で店舗を具体的にイメージした時に言及した通り、スターバックスが対象であるため、「テイクアウト」による売上を組み込まなければなりません。

また、計算対象が1日の売上であれば、平日のみを対象としてもよいでしょうが、1週間であれば、休日のパターンも計算しなければなりません。

複数パターンのフェルミ推定を実施する時間的な余裕はない

この時、ここまで計算してきた「イートイン」の計算と同様に、「テイクアウト」の場合も、数式の分解や数値の設定をしていくと、単純計算で2倍の時間がかかってしまいます。

しかし、ケース面接に与えられた時間は限られています。「イートイン」「テイクアウト」という、2つ以上の式の分解や数値計算をしている時間的な余裕はない場合も多いです。さて、どう対応すべきでしょうか？

【ポイント13】主要パターン以外は、係数を利用するなど、簡略に済ませる方法も考慮する

結論としては、係数などを利用して、簡略に済ませるアプローチを試しましょう。面接官から、2つ以上の式を検討するよう指示を受けたのでなければ、この「係数を利用する」方法で進めた方が現実的です。

「テイクアウトの売上」に対して、「テイクアウト率」の係数で対応する

今回の例だと、テイクアウトの売上を、どう計算すべきでしょうか。いくつかパターンを考えてみましょう。

パターン1： 正攻法で回答する

正攻法で実施する（普通にフェルミ推定式を構築する）と、かなり簡略的な式を作成した場合でも、以下のようになるでしょう。

しかし、この方法だと、1時間当たり客数の振れ幅が大きく、ここの数値を設定するために、様々な議論が必要になってしまいます。もっと簡略的に実施する、別の方法はないのでしょうか。

パターン2： テイクアウト率という項目を追加する

改めて、店舗をイメージしてみましょう。各時間帯にて、イートインの人、テイクアウトの人がそれぞれ存在します。さて、テイクアウトが占める割合という数値は、なんとなく、イメージできるのではないでしょうか。

せっかくなので、イートインの計算式に、このテイクアウト率というものを組み込んでしまいましょう。

・客数 = [席数] × [席の占有率] × [席の回転頻度] × [営業時間] ÷ [テイクアウト率]

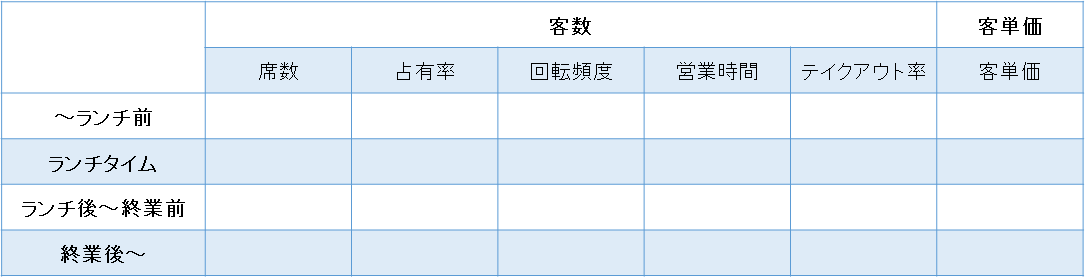
このような対応方法であれば、たとえイートインのみ（テイクアウトを見落とした状態）で、今までのような計算式や個別の数値設定が、すでにある程度終わった後であったとしても、それまで議論した内容や時間を無駄にすることなく、テイクアウトの売上を含めたうえで、議論を進められます。
　
上記の「パターン1」だと、1時間当たり客数は、お客さんの需要だけでなく、店舗がさばける数（イートイン需要のレジ客数）にも影響され、なかなか妥当な数値が計算しにくいです。このような場合、概算の数値を置くと、桁レベルで数値がずれてしまうリスクがあります。

しかし、「テイクアウト率」という数値は、おそらく数十パーセントであると思われ、大きくずれる可能性は小さいと思われます。
※イートインの客数が、テイクアウトの客数に影響を及ぼすことを考慮すると、そもそも、イートインとテイクアウトを、別々の計算式に分けるべきではないともいえます。

パターン3： そもそも、席数ではなく、レジ回転数で考える

そもそも、このテーマは「席の供給」をベースとした計算ではなく、「レジ・会計の供給」をベースとして計算したほうが適切とも思えます。

カフェの店舗をイメージすればわかりますが、ピーク時間帯は、席だけでなく、レジにおける会計も混雑しており、ここを供給制限として、計算の起点とすれば、大きな数値の乖離を防ぐことができそうです。

また、「席の供給」だと、「イートイン」しかカバーできませんが、「レジの供給」であれば、「イートイン」と「テイクアウト」の両方をカバーできます。

仮に、レジの供給で式（特に客数）を分解すると、例えば以下のようになるでしょう。

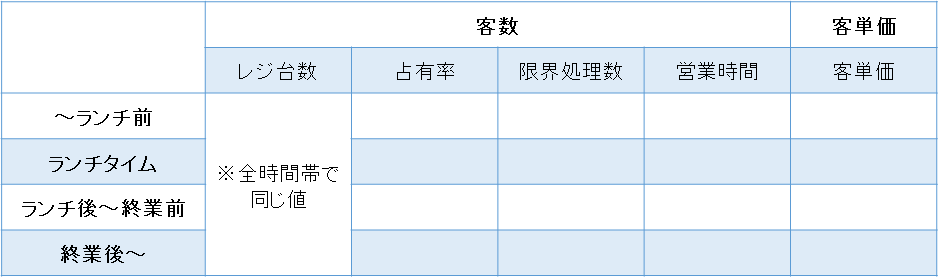
このように、どのような切り口が適切かを考えるうえでも、「ポイント3」において実施した具体的なイメージが重要です。

抽象的に考えているだけでは、なかなか、「席とレジという、複数の切り口がある」ということに気が付くことは困難です。そのような場合、「たまたま先に思いついた方の切り口に飛びつく」といった形で、切り口を決めて計算を進めることになってしまい。きわめてリスクが高いです。

途中で気が付いた場合の対応としても、「パターン2」のような係数対応は有効

上記の3種類のパターンを、思考力・論理性などの視点で比較すると、「パターン3」か「パターン2」のどちらかで解くのが、筋が良いと思います。

この時、最初から「パターン3」で解いていればBestですが、短時間の1回勝負であるケース面接では、そう理想的にいかない場合も多いでしょう。

このように、途中で重要な視点（テイクアウト）に気が付いた場合も含め、パターン2のように、係数で対応するというのは、非常に現実的かつ有効な対応策です。ぜひ覚えておいてください。

必ず、主要な方のフェルミ推定を実施する

さて、ここまで「係数で対応すればよい」という話をしていましたが、1週間の売上金額を計算する場合の、「平日」と「休日」のパターンの場合はどうでしょうか。

計算式が一緒であれば、両方ともフェルミ推定しても、大きな問題はない

さて、平日と休日は、時期の違いに過ぎません。そのため、分解した計算式（Step3までの検討）は、基本的に同じになると思われます。そのため、違うのは各項目に設定する数値（Step4以降）だけです。

「イートイン」と「テイクアウト」では、先ほどの「パターン1」の計算式ように、設定する数値だけでなく、計算式（Step2以降）から異なりました。そのため、両方ともフェルミ推定を実施する手間が大きいです。

しかし、今回の平日と休日は、式の分解そのものは同じであり、設定する数値が異なるだけです。これであれば、両方ともフェルミ推定を実施しても、大きな問題はないでしょう。（1週間であれば、平日側に×5、休日側に×2をする）

同じような議論を2回する意味も、あまりない

ただし、計算式が同じであるということは、議論する内容がだいたい同じになるということでもあります。短い30分の面接時間で、同じような議論を平日側と休日側で2回も行うことは、「ケース面接は自分の思考力をアピールする場である」という観点からすると、あまり意味がないと言えるでしょう。

主要な方のフェルミ推定に、係数補正を行う

上記のような理由から、「平日」「休日」も係数で対応してもよいでしょう。

しかし、このような場合、必ず、主要な方をフェルミ推定したうえで、主要でない側を係数で対応するというのが現実的です。

今回の場合、以下の観点から、平日側の方が1週間の売上金額に占める割合が大きく、「主要」と言えるでしょう

そのため、休日の売上金額の計算の方は、あまり重要ではないといえるでしょう。

例えば、まず平日1日の売上を計算したのち、この数値に0.8など、1より小さい数値をかけたものを、休日1日の売上にするなどの対応をしましょう。

もしくは、そもそも休日の売上に占める割合は小さいので、平日1日の売上に7をかけて、1週間の売上としても、あまり問題ないでしょう。
（※しかし、その場合であっても、あくまでケース面接は、数値の計算ではなく思考力を見るテストですので、「休日の方が、売上が小さいですが、簡易的に平日と同じ程度として計算します」といった形で、「平日の方が休日より売上が小さい」という視点に、言及しておく方が良いでしょう。）

一方、休日側を細かくフェルミ推定して、平日側を係数で簡略的に済ませるのはNGです。これでは、目的数値である売上金額の数値の曖昧さが大きくなってしまいます。必ず、論理的に考えて、主要な方を、フェルミ推定しましょう。

主要な方から、先にフェルミ推定を実施する

この原則は、両方ともフェルミ推定する場合でも同様です。あなたは、平日と休日の両方をフェルミ推定する予定であったとしても、色々と面接官と議論していくうちに、時間が足りなくなるかもしれません。

この時、先に平日側から計算していれば、結果的に時間が無くなった場合、休日側を係数対応しても、最終結果に与える影響は小さいです。しかし、先に休日側から計算していると、曖昧さが大きい、イマイチな最終結果になってしまいます。

「どちらを計算するか」も重要ですが、「先にどちらを計算するか」も、意識しながらアプローチしてください。

面接官から指摘を受けた場合に、初めて細かく計算する

もちろん、簡略的に係数で対応しようとしたときに、面接官から「そこをもっと詳しく計算して」と言われることもあります。「どうしてその係数にしたの」といった程度であれば、理由の説明で済みますが、「計算」するように指示を受けた場合は、フェルミ推定をしましょう。

あくまで、フェルミ推定は思考力を見るテスト。最終回答を出すことばかりにこだわらない

繰り返しますが、ケース面接は「思考力を見るための試験」にすぎません。面接官からすれば、「最終回答を導出する」ことよりも、「思考力をはかる様々な機会を作り出す」ほうが有用です。おそらく、このまま最終解答を導出するよりも、もう一つのフェルミ推定・計算を見るほうが、有効と判断したのでしょう。

必ずしも、最終結果導出のために、論理的な意味があることのみを実施すればよいわけではないと、意識してください。あくまで、実施すべきなのは、「あなたの思考力の高さを、面接官に表現・理解してもらうこと」です。

では最後に、今回の記事の要点を改めてまとめると下記3点です。

さて、次回のコラムでは、次のStep7の解説を行っていきます。次回で「原則編」はラストになりますので、併せてご覧ください。

---