目次
戦略コンサルの筆記試験を突破するには？
こんにちは、外資就活 コンサルチームです。
今回は戦略コンサルの最難関の選考フローの一つである筆記試験（Webテスト）について解説します。
戦略コンサルの筆記試験は難易度が高く、中には「どれだけ対策をしても解けるようにならない」「問題集の解説が丁寧でない」といった理由で、なかなか対策が進まないと悩む方も多いのではないでしょうか。
多くの問題集では「このように整理するとうまく解けます」という解説はあっても「なぜ、そのように整理するのがよいのか」と丁寧に説明されているわけではありません。そこで今回は、「なぜ、そのように整理するのがよいのか」に力点を置いて、例題を通じて解き方を解説していきたいと思います。
問題数は少ないですが、どこが正解と不正解の分かれ目になるのか、具体的かつ丁寧に解説します。
戦略コンサルの筆記試験は難関
問題の解説に入る前に、戦略コンサルの筆記試験についておさらいしておきましょう。
戦略コンサルの筆記試験は、ファームによっては通過率10%程度となる難関のステップであり、入念な対策が必要です。
コンサル志望者の中には「学歴が高ければ筆記試験に落ちることはない」と思っている方もいることでしょう。しかし実際には、東大生でも例年かなりの方が筆記試験で落ちています。せっかくケース面接の対策を入念に行ったとしても、筆記試験で落ちてしまったらその労力も水の泡です。油断せずに対策を行いましょう。
コンサルの筆記試験はファームによって試験形式が異なるため、様々な試験形式に対応できるような対策が必要です。各ファームの筆記試験についてご存じない方は、こちらの【戦略コンサル内定】Webテスト対策まとめ｜SPI・TG-WEB・玉手箱・独自形式もぜひご覧ください。
例題と解説
取り上げた問題と解説方針について
多くの問題集では、それぞれの問題の解き方について、「どのように整理すれば解けるか」「最初にどの条件を考えると解けるか」については非常に丁寧に説明されています。一方で、「なぜ、そのような整理をするのか」「なぜ、最初にその条件を記入するのか」についての解説はほとんど行われていません。
そこでこのコラムではこの2点に焦点を当て、特に難解とされている判断推理について詳しく解説していきます。
今回は解法が他に応用可能かつ質の高い問題を2問取り上げました。筆記試験に苦手意識のある方は、紙とペンを用意して例題を実際に解いてから、解答を読み進める事をおすすめします。
なお、判断数理の対策に関しては、こちらの【判断推理・数的推理対策】 国家総合職＆コンサル志望者向け！ 超効率的攻略法もぜひご覧ください。
第1問
ある幼稚園では、図のように4人ずつのグループで円卓を囲んでお弁当を食べる。ある日のA～Dの4人のお弁当に入っているおかずの種類を数えると、ハンバーグ、ベーコン巻き、春巻き、トマト、ブロッコリー、ポテトサラダの6種類だった。どの子供のお弁当にも、いずれか3種類ずつが入っており、向かいの人と同じおかずは1つもないが、隣の人とは同じおかずが少なくとも1つあった。4人のお弁当のおかずについて次のことがわかっているとき、確実に言えるのはどれか。
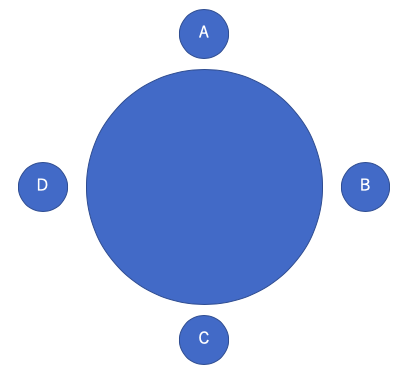
Aには、ハンバーグとポテトサラダが入っていた。
Bには、Aと同じおかずが2つあった。
Cには、トマトと春巻きが入っていた。
Dには、春巻きもブロッコリーも入っていなかった。
【回答の選択肢】
1. AとBのお弁当には、どちらもブロッコリーが入っていた。
2. AとDのお弁当には、どちらもハンバーグが入っていた。
3. BとCのお弁当には、どちらもハンバーグが入っていなかった。
4. BとDのお弁当には、どちらもポテトサラダが入っていなかった。
5. CとDのお弁当には、どちらもポテトサラダは入っていなかった。
（引用元：https://www.jinji.go.jp/saiyo/siken/mondairei/14_1.pdf）
第1問の答えと解法
問題文の制約条件は、
ii. 向かいの人と同じおかずは1つもない。
iii. 隣の人と少なくともおかずが1つ同じである。
の3点です。
また、わかっていることとして
v. Bには、Aと同じおかずが2つあった。
vi. Cには、トマトと春巻きが入っていた。
vii. Dには、春巻きもブロッコリーも入っていなかった。
が挙げられています。
そこで今回は、下図のような「表」を作って整理することにしました。
表形式で整理することの利点として、
・各人のおかずの種類（今回は◯で表しました）を確認しやすいこと
・おかずごとに把握できること
の2点があります。
それでは問題を解いていきましょう。
まずは、与えられた条件からわかる情報を、わかる範囲で全て反映させます。わかっている情報のうち、書き込めるものは全て記入するのが基本中の基本です。
ただし、この時点ではまだAとBのおかずについてわかっている情報が少なすぎるため、「v. Bには、Aと同じおかずが2つあった。」は使っていません。
次に、上に整理した条件と、「ii. 向かいの人と同じおかずは1つもない。」という条件を満たすように穴を埋めます。（なお、以下では新たに記入した箇所を青く表示します）
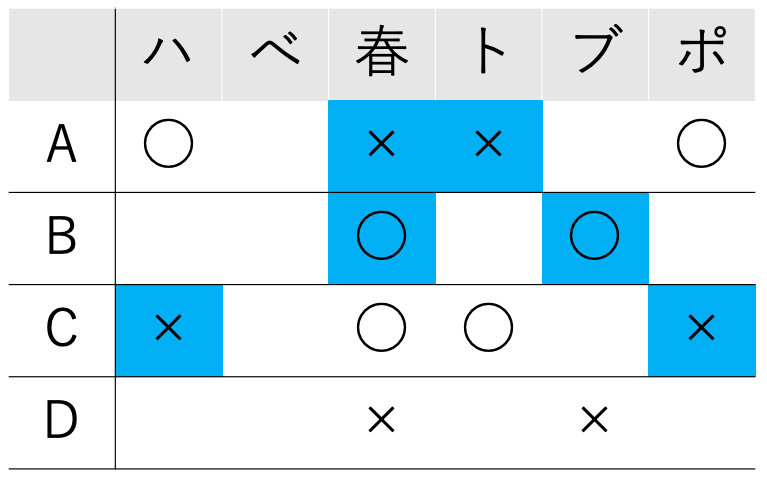
ここで、AとBについて、まだ使っていない「5. Bには、Aと同じおかずが2つあった」という条件を考えます。
上記の条件を満たすパターンは3つあります。
②A-ブとB-ポが◯
③B-ハとB-ポが◯
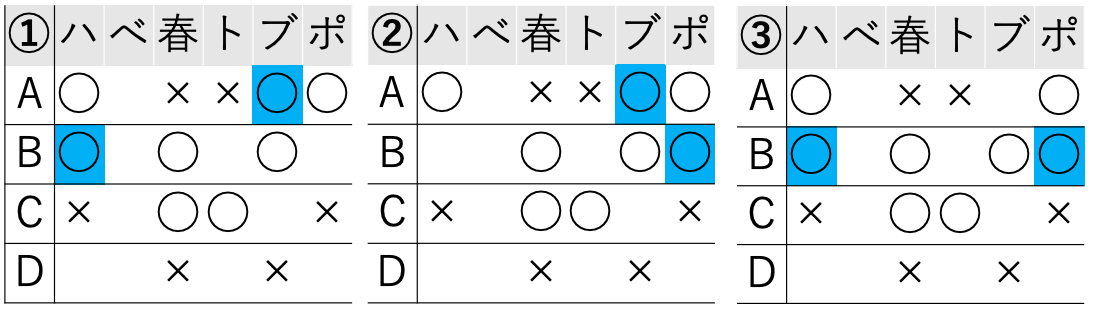
ただし、③に関してはBに◯が4つついてしまいましたので、今後は考慮せず、①と②を考えていきます。
①について
まず、「i. 各人のおかずは3種類である」という制約条件を利用すると、Aは既に3種類のおかずが確定しているので、Aにベーコンは入っていないことが分かります。また、同様にBも3種類のおかずが確定しているので、Bにベーコン、トマト、ポテトサラダは入っていないことが分かります。
さらに、「ii. 向かいの人と同じおかずは1つもない」という制約条件を利用すると、AとBのおかずは既に確定しているので、CとDのおかずは以下のように定まります。
②について
②も➀と同様に、A, Bは既におかずが3種類確定しているので、
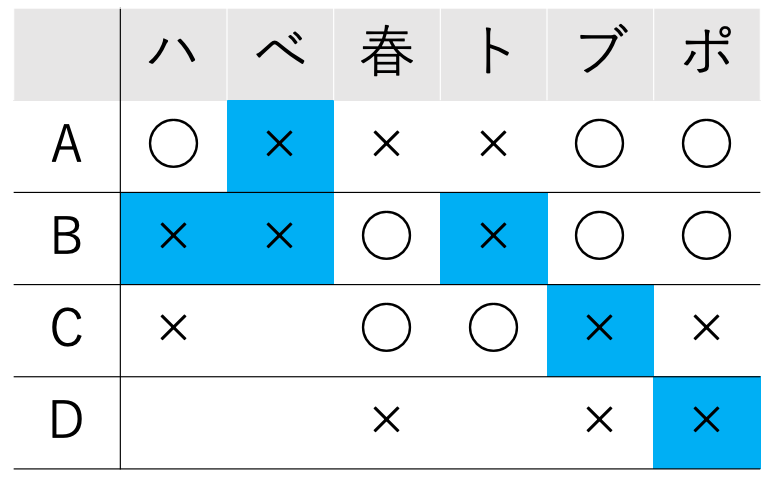
と表を埋めることができます。
さらに、「ii. 向かいの人と同じおかずは1つもない」という制約条件を利用すると、AとBのおかずは既に確定しているので、CとDのおかずは以下のように定まります。
以上➀、②の議論より、選択肢の中でこれらに合致するのは、
選択肢1：「AとBのお弁当には、どちらもブロッコリーが入っていた。」
のみになります。
というわけで、第1問は選択肢1が答えです。
第2問
ⅰ）Sの順位は、Rより下である
ⅱ）Pの順位は、Qより下である
ⅲ）Tの順位は、Rよりも上だが、1着ではなかった
ⅳ）同着の者はいない
さらにどのような情報が追加されれば、5人の着順が全て決まるか。ただし、情報として追加する選択肢は、できる限り抑えるものとする。
【回答の選択肢】
ア）Tは2番目に到着した
イ）Rは3番目に到着した
ウ）Sは4番目に到着した
（オリジナル）
まず、整理の方法から考えます。順位の問題は、多くの場合、今回のような相対的な順位の差で提示されることが多いです。そのため、
・R→S
・Q→P
・T→R
のような書き方だけメモをする人もいます。しかしこれでは、
・ⅲ）Tの順位は、Rよりも上だが、1着ではなかった
や、
・Aさんの順位はBさんよりも2つ高い
などのひねりがある条件をわかりやすく表現することができません。
そこで今回は、各順位ごとの枠を作って、場合分けをする形式で整理してみました。
次に、4つの条件のうちどれから記入するかを考えます。
ⅱ）Pの順位は、Qより下である
ⅲ）Tの順位は、Rよりも上だが、1着ではなかった
ⅳ）同着の者はいない
「ⅰ）Sの順位は、Rより下である」を最初に記入すると、10パターンあります（ⅱも同じく10パターンであることはお分かりいただけるかと思います）。
一方「ⅲ）Tの順位は、Rよりも上だが、1着ではなかった」を最初に記入すると、Tが1位でないという制約条件がついているため、6パターンに絞られます。
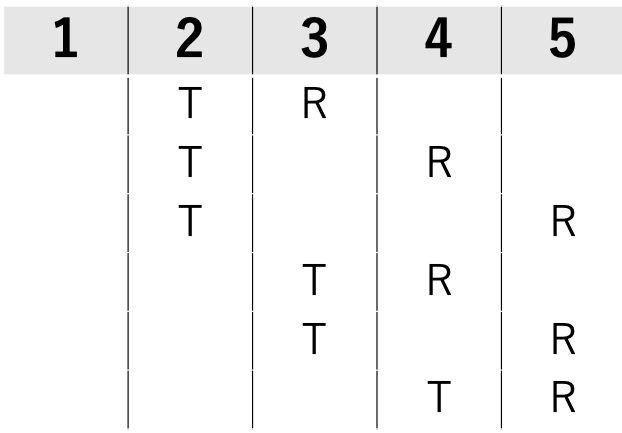
そのため今回は、ⅲから記入していきます。このように、なるべく制約が大きい条件から記入していくと、整理しやすくなります。
次に使える条件を考えます。
ⅰとⅲが残っていますが、この時点で記入している部分（T, R）と組み合わせられる条件があると記入しやすくなります。
そこで、ⅰを記入すると、Rよりも下位に余地がある4パターンに絞られます。
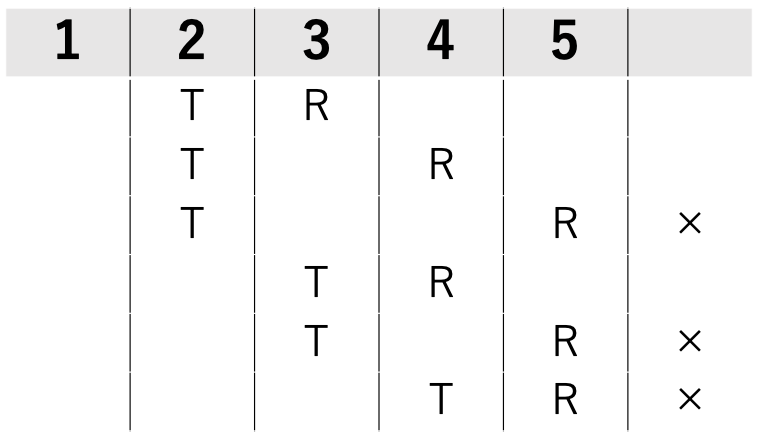
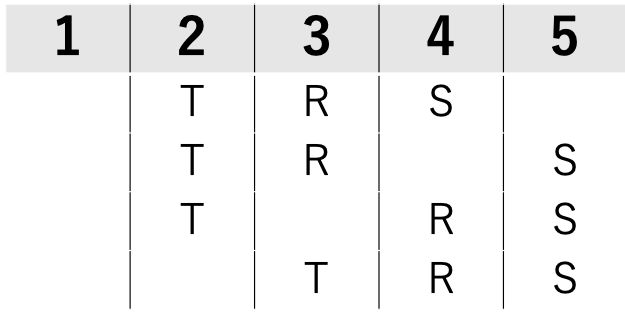
すると、残りの空いている部分2カ所に、Q→Pの順に入ることが分かると思います。
ここまで記入できたら、最初の選択肢を見てみましょう。
イ）Rは3番目に到着した
ウ）Sは4番目に到着した
上の表と照らし合わせると、1つに絞り込めるのは
ウ）Sは4番目に到着した
だけになります。というわけで、第2問は選択肢ウが答えです。
戦略コンサルの筆記試験突破のコツは「情報の図解」
いかがでしたか。
今回のコラムでは筆記試験でつまづきがちな問題を取り上げて詳しく解説しました。
今回取り上げた問題以外も、分かる情報から図解しつつ整理していけば解くことができます。ぜひご自身でやってみてください。
筆記試験対策を万全にして、ケース面接やジョブに進めるようにしましょう！
マッキンゼー ゴールドマン 三菱商事
P&G アクセンチュア
内定攻略 会員限定公開
トップ企業内定者が利用する外資就活ドットコム
もっと記事を読む
マッキンゼー BCG ベイン・アンド・カンパニー アクセンチュア 等の内定攻略記事を会員限定に公開しています
